この記事を読んでくれているあなたは、
◆材料力学が苦手。
◆はりの三角分布荷重の問題の解き方が分からない。
◆SFD、BMDが書けない。
という悩みを抱えていませんか?
この記事では、三角分布荷重を理解するために5つの重要ステップに分けて解説しています。 図解多めなので、材料力学が苦手な方でもイメージがしやすいと思いますよ!
ぜひ一緒に勉強していきましょう!
ちなみに今回解説する問題は、教科書「改訂新版 図解でわかるはじめての材料力学」の演習問題です。
YouTubeでも解説動画ありますのでぜひ。 youtu.be
材料力学の三角分布荷重のはりの問題って?
片持ち梁ではいろいろと種類があります。
初級として、集中荷重と等分布荷重の問題が解ければOKだと思います。
続いて中級では、おもりが三角形になっている場合を考えましょう!
少し難しく感じますが、しっかりとステップ毎に理解を深めていきましょう!
材料力学のはりの解き方(三角分布荷重)

今回は、↑のような三角分布荷重がかかる片持ち梁の問題の解き方をステップ毎に解説します。
基本的な考え方は等分布荷重の解き方と同じです。(等分布荷重の解き方の復習はこちらからどうぞ)
しかし、三角分布荷重の場合は1点だけ新たなステップが必要です。
三角分布荷重の場合は合計5つに重要ステップにまとめました。この5つの手順に従って解説していきます。
①板の左端を原点として、右向き正の軸[m]をとる
②刀で板を切って仮想的な断面を作る
③おもりについて、単位長さあたりの重量-距離のグラフを書く
④等分布荷重を集中荷重に置き換える
⑤仮想的な断面の✖印にかかる力とモーメントを考える
この5ステップの順番通りにすれば、はりの三角分布荷重の問題は必ず解けます。
それでは、実際に考えていきましょう!
はりの三角分布荷重を解く時のステップ①:右向き正の 軸[m]をとる
軸[m]をとる
はりの問題を解く時は毎度おなじみの考え方です。
板の左端を原点として、右向き正の軸[m]をとりましょう。
はりの三角分布荷重を解く時のステップ②:刀で板を切って仮想的な断面を作る
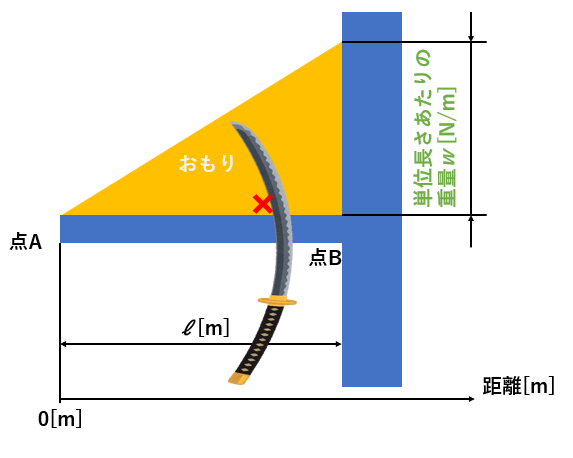
まずは三角形のどの部分でもいいので、おもりを刀で切りましょう。↑
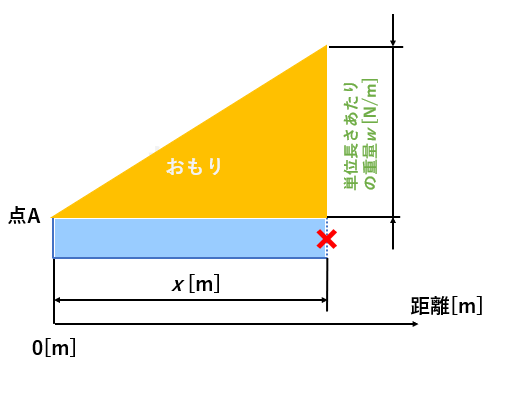
おもりの横幅は任意なので[m]になりますね。
ただ、このままでは梁の問題を解くことはできません。
ステップ③とステップ④が非常に大事になります。
順にみていきましょう。
はりの三角分布荷重を解く時のステップ③:おもりについて、単位長さあたりの重量-距離のグラフを書く
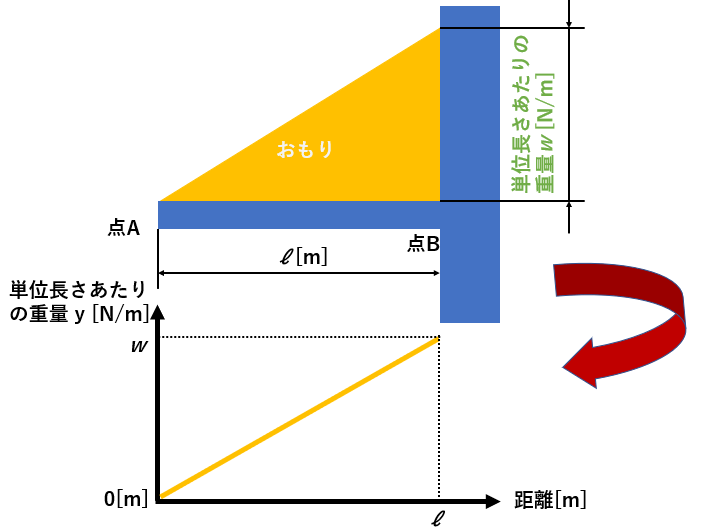
重要なステップ④に行く下準備としてステップ③をしていきましょう。
ステップ③ではこの黄色のおもりについて、横軸は距離[m]、縦軸は単位長さあたりの重量[N/m]の直線のグラフを書きましょう。
間違いやすいポイントですが、縦軸は[N]ではなく[N/m]です。
単純におもりの横の長さと縦の長さの関係をグラフに表したと考えてください。
それでは、この1次関数のグラフの傾きはいくらでしょうか?
そうですね、直線の傾きはになりますね。これをステップ④で使います。
はりの三角分布荷重を解く時のステップ④:等分布荷重を集中荷重に置き換える
皆さん、集中荷重なら解くことができますよね。(もしも忘れてしまった方は先にこちらから復習しましょう)
三角分布荷重は難しそうに見えますが、集中荷重に直して解いていこうという考え方です。
いよいよ三角分布荷重の問題を解くにあたって最大の重要ポイントを説明します。
集中荷重の大きさ→三角形のおもりの面積
集中荷重の位置→全体のの位置
それでは、↑の三角形のおもりの面積を考えましょう。
横幅は[m]、縦幅は
ですので、三角形の面積は、
と計算できますね。
これが集中荷重に直した時の重量です。
また、この集中荷重がかかる位置ですが、右端からの場所です。
※これは三角形の重心は2:1になるということに由来します。
↓の図が三角分布荷重から集中荷重に直した図です、自分が書いた図と確認してみてください。
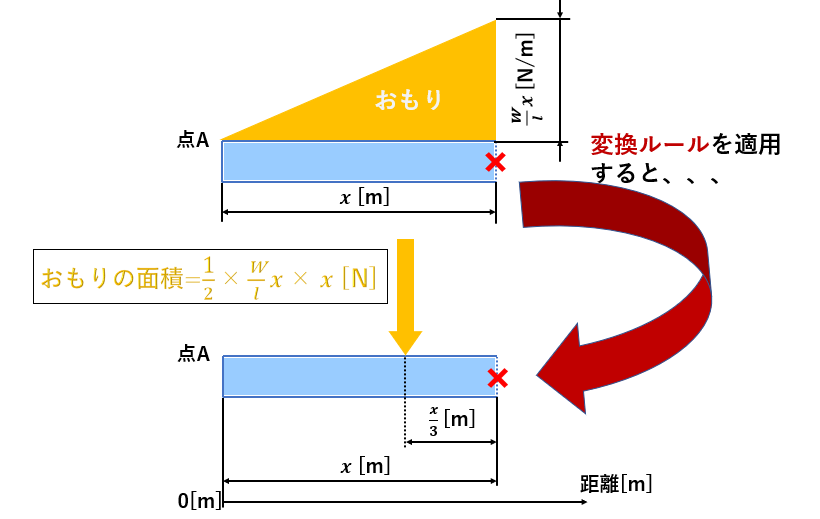
ここまでできれば後はもう簡単です。仮想断面にかかる力とモーメントを求めていきましょう。
はりの三角分布荷重を解く時のステップ⑤:仮想的な断面の✖印にかかる力とモーメントを考える
集中荷重や等分布荷重と解き方同じなので簡単に説明して、SFDとBMDのグラフを書いていこうと思います。
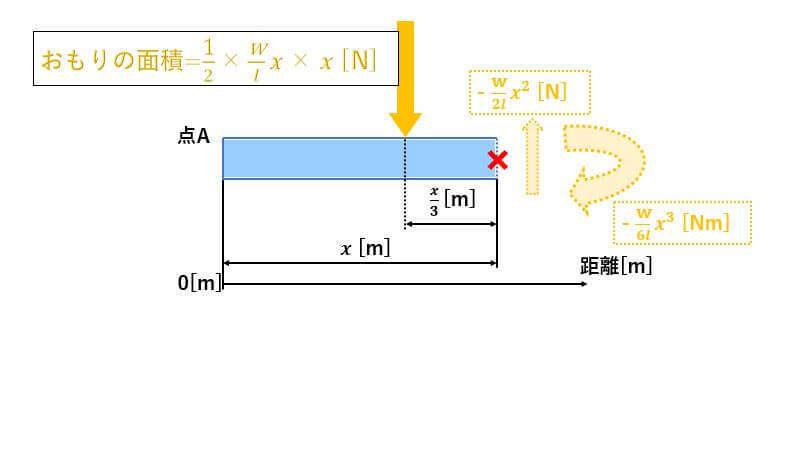
せん断力 [N] ・・・(1)
曲げモーメント [Nm]・・・(2)
※もしもせん断力や曲げモーメントの符号の決め方が分からなくなった場合はぜひこちらから復習しましょう。
材料力学のはりの問題のメイン:SFDとBMDグラフを書こう!
SFDのグラフの書き方
再度SFDのグラフを書く時のポイントをまとめました。
・横軸は原点からの距離[m]
・縦軸はせん断力[N] (上向き正)
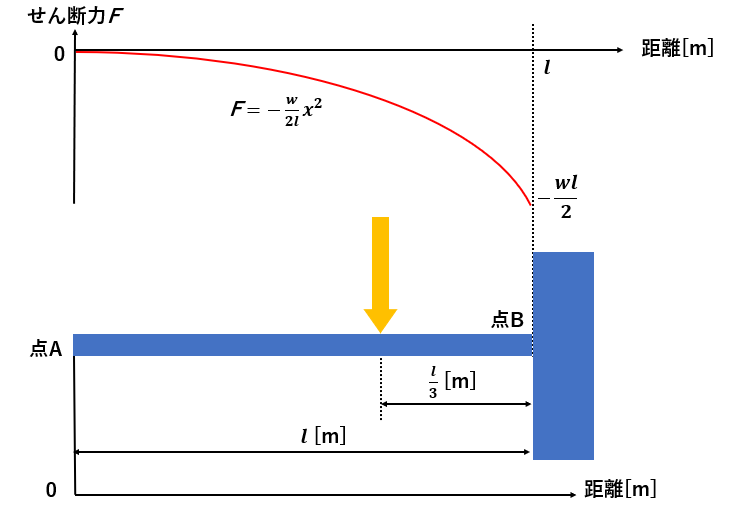
BMDのグラフの書き方
横軸は原点からの距離、縦軸は曲げモーメントとしてください。
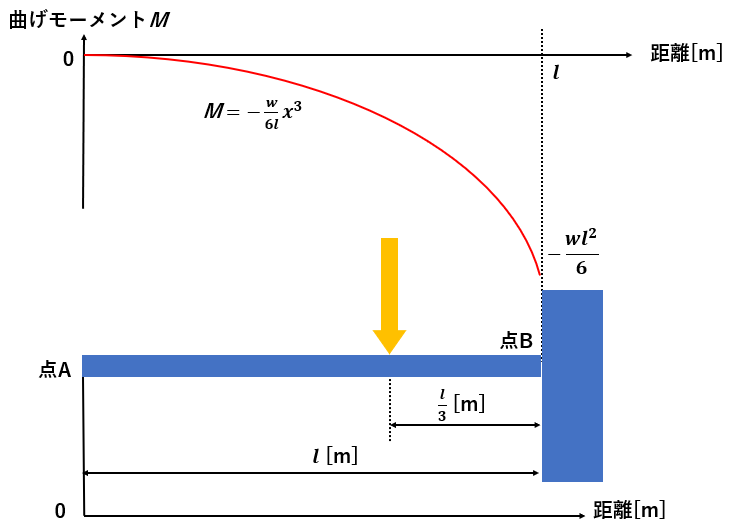
BMDのグラフ理解できたでしょうか?
材料力学のはりの問題まとめ

いかがだったでしょうか?
はりの三角分布荷重の問題は中級レベルでしたが、完ぺきにクリアできたでしょうか?
何度も復習して頑張っていきましょう!
また材料力学を勉強する上でおすすめの参考書を2冊ご用意しました。
「マンガでわかる材料力学」は、kindleバージョンもあって個人的におすすめ。iPadとの相性も◎
こちらは材料力学のテスト勉強に最適です
☆ iPadがある大学生活のメリット10選はこちらの記事よりどうぞ
iphoneとiPadの2台持ちが超便利な理由10選!【iPadを5年以上使っています】
材料力学の公式集や、不静定問題・はりの等分布荷重の解き方を丁寧に解説した記事も作りました。ぜひついでに勉強しましょう!
また、解説してほしい材料力学の問題がありましたらFollow @OribiStudyのDMでご連絡ください。ありがとうございました。





