おりびのブログ

「機械工or院卒→開発部」を目指す理系のためのブログ。

機械工学科

材料力学の問題解説

研究室

買ってよかった物

【材料力学の重要公式】材料力学の単位を取るために必ず覚えたい公式集

材料力学の解説

この記事を読んでくれているあなたは、

◆材料力学が苦手。

◆材料力学で重要な公式をサクッと知りたい。

といった方向けの記事です。

材料力学ってたくさん重要公式が出てきますし似ている式が多くて間違いやすいですよね。

しかし毎回教科書で公式を探すのも大変だと思います。

この記事ではオリジナルな図を使って、公式と式の意味をセットでまとめました。これで理解しやすくなると思います。

テスト前の方や久しぶりに材料力学を勉強し直している方はぜひチェックしてください。

それではさっそく材料力学の勉強を始めましょう。

YouTubeでも解説動画ありますのでぜひ。 >>材料力学を習う意義

材料力学の公式

材料力学公式

材料力学の公式は、そこまで多くはありません。

しかし積分が入っていてややこしかったり紛らわしい公式もあるので、図を見ながらイメージして式を覚えていきましょう！

応力・ひずみ・フックの法則の公式

応力

材料力学を習う中で応力は最も基本かつ重要な勉強です。

応力は、垂直方向に力がかかっているのか平行方向に力がかかっているのかで２種類に区別します。

順に２つの応力についてみていきましょう。

垂直応力

$\sigma = \displaystyle \frac{N}{A}$

$\sigma$ : 垂直応力、N : 仮想断面に垂直な内力、A : 断面積

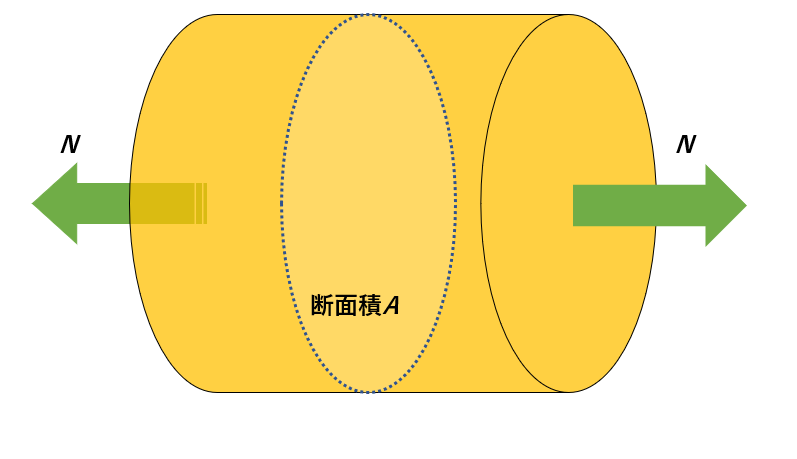
材料力学公式

ある物体の断面に対して垂直な力Nが加わっている場合の垂直応力 $\sigma$ の関係式です。

引っ張る、押しつぶすような力が働いていますね。　

せん断応力

$\tau = \displaystyle \frac{F}{A}$

$\tau$ : せん断応力、 $F$ : 仮想断面に平行な内力、 $A$ : 断面積

材料力学公式

ある物体の断面に対して平行な力Fが加わっている場合の垂直応力 $\tau$ の関係式です。 引きちぎるような力が働いていますね。

ひずみ

変形の度合いを表す無次元量としてひずみがあります。

これも、縦方向(長さの比)と横方向(直径の比)でひずみは２種類あります。

順番に２つのひずみについて解説していきます。

縦ひずみ

$\varepsilon = \displaystyle \frac{l- l_{0}}{l_{0}} = \displaystyle \frac{\lambda}{l_{0}}$

$\varepsilon$ : 縦ひずみ、 $l$ : 変形後の棒の長さ、 $l_{0}$ : 棒の元の長さ

材料力学公式

縦ひずみ $\varepsilon$ は、棒の長さ方向について考えています。

※かなり棒が伸びたように見えますが、材料力学の世界ではこんなに伸びません。弾性領域のみを考えるので、変形量は微々たるものです。

元の棒の長さが $l_{0}$ だったのに対し、引っ張ると $l$ のなった時の変形の割合を縦ひずみ $\varepsilon$ で表しています。

横ひずみ

$\varepsilon^{ '}= \displaystyle \frac{d- d_{0}}{d_{0}}= \displaystyle \frac{Δd}{d_{0}}$

$\varepsilon^{ '}$ : 横ひずみ、 $d$ : 変形後の棒の直径、 $d_{0}$ : 棒の元の直径

材料力学公式

横ひずみ $\varepsilon^{ '}$ は、直径の変化について考えています。棒の元の直径が $d_{0}$ だったのに対し変形後 $d$ になった場合の直径の変形割合を考えています。

フックの法則

フックの法則も、縦方向と横方向で２つ大事な式があります。

縦ひずみとヤング率

$\sigma = E\cdot\varepsilon$

$\sigma$ : 垂直応力、 $E$ : ヤング率(縦弾性係数)、 $\varepsilon$ : 縦ひずみ

材料力学公式

縦ひずみ $\epsilon$ とヤング率 $E$ は、有名なばねのフックの法則とよく似ていますね。

せん断ひずみとせん断弾性係数

$\tau = G\cdot\gamma$

$\tau$ : せん断応力、 $G$ : せん断弾性係数、 $\gamma$ : せん断ひずみ

材料力学公式

伸び

伸び

$\sigma = \displaystyle \frac{P}{A} = \displaystyle \frac{\lambda}{l}E$

となる。 $\lambda$ について解き直すと、

$\lambda= \displaystyle \frac{Pl}{AE}$

$\sigma$ : 垂直応力、 $\lambda$ : 伸び、 $l$ : 棒の長さ、 $P$ :荷重、 $A$ :断面積、 $E$ :ヤング率

不静定問題を解く時は、 $\lambda$ を求めることが必須になり↑の式は非常に重要です。 不静定問題の復習はこちら

安全率

安全率

$\sigma_a = \displaystyle \frac{\sigma_s}{f}$

$\sigma_a$ : 許容応力、 $\sigma_a$ : 基準応力、 $f$ : 安全率

安全率の考え方は非常によく使いますしテストにも出ます。

安全率は１よりも大きい数字で、点検回数や高温環境、危険性を考慮して決めます。

エレベーターは年に数回しか点検できないので安全率は高めの10ぐらいです。

しかし飛行機の場合、機体の重量を小さくするために安全率は1.5前後です。毎回部品点検を行うことで安全率を低く設定しています。

許容応力 $\sigma_a$ と基準応力 $\sigma_a$ のどっちがどっちだったか分からなくなりがちです。

2つの中でより小さい値(許容応力 $\sigma_a$ ) を設計では使うと覚えておきましょう。

熱応力の公式

熱応力

$\lambda = l\alpha \Delta t$

$\lambda$ : 伸び、 $l$ : 棒の長さ、 $\alpha$ : 線膨張係数、 $\Delta t$ : 温度変化

材料力学公式

物体を熱すると膨張し、冷やすと収縮します。

その変形量を表した式です。

また、温度変化 $\Delta t$ は $t_1$ → $t_2$ を表していますので、 $\Delta t$ がプラスだと膨張、 $\Delta t$ がマイナスだと収縮を表します。

　

円形断面のねじりの公式

断面二次極モーメント

断面二次極モーメント

$I_p = \int r^{2} dA$

$I_p$ : 断面二次極モーメント、 $r$ : 半径、 $A$ : 断面積

断面二次極モーメント $I_p$ は断面の形のみで決まる値であり、ねじれの問題でよく出てきます。

ねじりで重要な４つの公式

ねじりの神４式

$\gamma =R \theta$

$\tau = G \gamma$

$T = G \theta I_p$

$I_p = \int r^{2} dA=\displaystyle \frac{\pi}{2}R^{4}$

$\gamma$ : せん断ひずみ、 $R$ : 半径、 $\theta$ : 比ねじれ角、 $\tau$ : せん断応力、 $G$ : せん断弾性係数、 $T$ : ねじりモーメント、 $I_p$ : 断面二次極モーメント

↑の４つの式を使って式変形するとねじりの問題は必ず解けます。

はりの公式

はりの曲げ応力の公式

曲げ応力

$\sigma(y) = \displaystyle \frac{M(x)}{I}y$

$I= \int y^{2} dA$

$\sigma(y)$ : 垂直応力、 $M(x)$ : 曲げモーメント、 $I$ : 断面二次モーメント、 $y$ : 中立軸からy方向の距離

$I$ は断面二次モーメントです、断面二次極モーメントと間違いやすいので気を付けましょう。

はりのたわみ

はりのたわみ

$EI \displaystyle \frac{d^{2}y}{dx^{2}}= -M(x)$

$E$ : ヤング率、 $I$ : はりの断面二次モーメント、 $M(x)$ : 曲げモーメント

↑の微分方程式を１回積分すると、たわみ角 $i$ = $\displaystyle \frac{dy}{dx}$ が、 ２回積分すると、たわみ $y$ を得ることができます。

長柱の座屈応力の公式

座屈応力

$P= C \displaystyle \frac{ \pi^{2} EI}{l^{2}}$

$P$ : 座屈荷重、 $C$ : 拘束係数、 $E$ : ヤング率、 $I$ : 断面二次モーメント、 $l$ : 柱の長さ

$C$ は拘束係数と呼ばれ、柱の拘束状態で決まる定数です。

一端固定支持、他端自由　　　→ $C$ = 0.25　

両端固定支持　　　　　　　　→ $C$ = 1

一端固定支持、他端回転支持　→ $C$ = 2.0458 $\fallingdotseq$ 2

両端固定支持　　　　　　　　→ $C$ = 4

　

材料力学の重要公式まとめ

材料力学の重要な公式をまとめました。勉強に役立ててください。

また材料力学を勉強する上でおすすめの参考書を2冊ご用意しました。

「マンガでわかる材料力学」は、kindleバージョンもあって個人的におすすめ。iPadとの相性も◎

マンガでわかる材料力学

末益博志, 長嶋利夫【著】オーム社出版マンガシリーズに材料力学が登場！変形や強度を考えてみよう！

　こちらは材料力学のテスト勉強に最適です

演習材料力学 (セミナーライブラリー機械工学)

尾田十八, 三好俊郎【著】サイエンス社出版大学のテスト勉強に最適！

☆ iPadがある大学生活のメリット10選はこちらの記事よりどうぞ

iphoneとiPadの2台持ちが超便利な理由10選！【iPadを5年以上使っています】

　　　　　　

　　

はりや不静定問題の解き方を図解ありで分かりやすく解説した記事を作りました。テスト前の方はぜひこちらもご覧ください⇩

合わせて読みたい！

また、解説してほしい材料力学の問題がありましたらFollow @OribiStudyのDMでご連絡ください。ありがとうございました。

機械工のあなたにおすすめの記事

　

おりびのブログはリンクフリーです

当サイトは管理人の許可なくリンクを張って頂いて問題ございません。
内容をコピー、スクリーンショットや画像のご利用も、該当記事へ「出典」としてリンクを張っていただければ問題ございません。
おりびのブログのホーム画面に戻る