この記事を読んでくれているあなたは、
◆材料力学が苦手。
◆不静定問題の解き方が分からない。
◆仮想断面ってなに。
という悩みを抱えていませんか?
この記事では、最も基本的な不静定問題が20分でマスターできるように丁寧な解説を作りました。
それでは頑張って材料力学の勉強をしていきましょう。
ちなみに今回解説する問題は、教科書「改訂新版 図解でわかるはじめての材料力学」のp.48の演習問題です。
YouTubeでも解説動画ありますのでぜひ。 材料力学の不静定問題を分かりやすく!【4つのステップで必ず解ける!】
材料力学の不静定問題ってなに?

材料力学の勉強の中で、不静定問題が一番のメインと言っても過言ではないぐらい重要な内容です。
しかし、伸び縮み量 の求め方や、仮想断面に生じる内力の求め方が難しいですよね。
本記事では図解多めで丁寧に解説しています。
⇩の不静定問題を解きます!

ぜひ最後までご覧ください。
材料力学の不静定問題の解き方
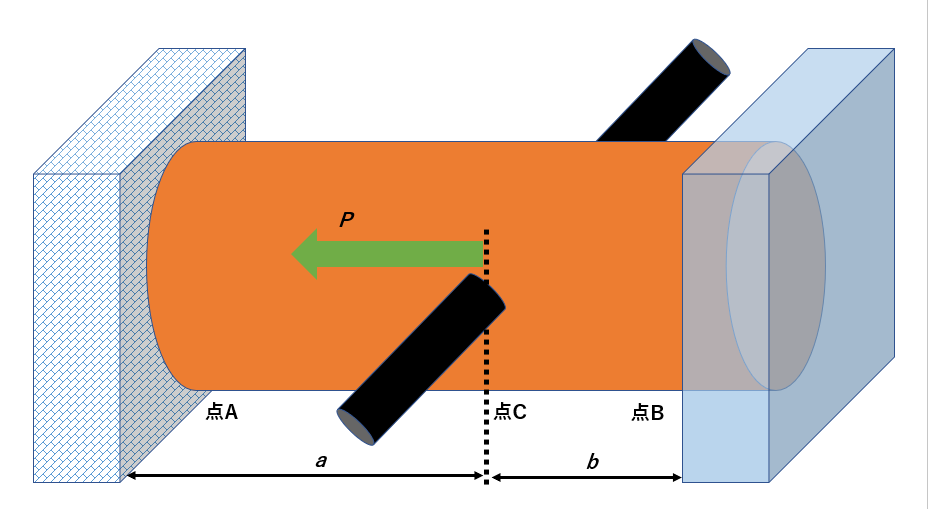
本記事では、引張り力と圧縮力が作用する不静定問題の詳しい解説をします。
↑の図のように剛体壁の間にオレンジ色の棒ABが無理なく固定されていて、その間のC点に荷重Pが加わる問題を考えます。
イメージとしては、オレンジ色の棒ABに黒い棒を突き刺して左方向に押しているような感じです。
その際、両端は剛体壁=動かない壁なので、オレンジ色の棒が左に移動することはありません。
また、両端の壁とオレンジ色の棒は引っ付いているので力を加えても外れることはありません。
(※溶接されていると思ってください。)
問題文のイメージができたところで、この不静定問題を解く重要ポイントを4つにまとめました。
②区間ACと区間CBの伸び縮みした量を考える
③仮想的な断面に生じる内力を考える
④伸び縮みした量について等式を立てる
この4つの手順に従って解説していきます。
不静定問題を解く時のステップ①:反力を仮定し、力のつり合い式を立てる
 まずは、このオレンジの棒の働いている反力を全て図示しましょう。
まずは、このオレンジの棒の働いている反力を全て図示しましょう。
まず点Cにおいて、力Pが左方向に加わってますね。
点Aでは力Pによって押されているので、力Pと逆向きの右方向に反力を仮定しましょう。
点Bでは、オレンジの棒が壁から離れようとしているけど引っ張って離れないようにしているので、右方向に反力を仮定しましょう。
ここまでは大丈夫でしょうか?
右方向には反力と反力
が、左方向には力Pが働いているので、右向き正として力のつり合い式を当てましょう。高校物理で習ったことをします。
これで第一ステップ終了です、続いて棒の伸び縮みした量について考えていきます。
不静定問題を解く時のステップ②:区間ACと区間CBの伸び縮みした量を考える
求めたい文字がと
の2つあるのに対し、式(1)1個だけでは解くことは不可能です。
そこでもう1つ式を立てなければいけません。
何について式を作るかというと、区間ACと区間CBの伸び縮みした量について式を立てます。
◆力のつり合い式だけで解ける問題を静定問題(高校物理)、
◆力のつり合い式だけは解けない問題を不静定問題という(材料力学)。
今回の問題では、力のつり合い式だけは解けず変形を考慮しなければいけないので不静定問題ですね!
では、具体的に変形を考えていきます。
不静定問題を解くにあたり重要な考え方は以下になります。
◆それぞれの区間で伸び縮みした変形量をλとする
◆実際壁は動かないので、オレンジ棒全体のの変形量は0になる
変形量λの式を覚えているでしょうか?
ヤング率は材料固有の値なのでただの定数です。
断面積は、今回のオレンジ色の棒は円柱状なので断面積も
で一定値です。
長さも簡単ですね、AC区間の長さはa、CB区間の長さはbですね。
問題は内力です。
外力や反力とは異なりますよ、ここが混乱ポイントです。
この内力が少々難しいですので順に考えていきます。
内力とは:仮想的な断面に分割し、その断面に作用する力のことです。
??
って感じですよね。
では、ステップ③で、仮想断面に生じる内力の求め方を詳しく解説します。
不静定問題を解く時のステップ③:仮想的な断面に生じる内力を考える
それではまず、一番難関の仮想的な断面に生じる内力を考える重要ステップをまとめました。↓
◆刀で好きなところを切る
◆切った棒の右側はないものと考える
◆仮想断面にどんな力が働いているか考える
まずはAC区間から考えましょう。AC区間の好きなところを刀で切ります。

AC区間を刀で切ると、↓のような図になります。

大事なことなのでもう一度言いますが、刀で切った右側の部分はないものと考えてください。
↑の図の点線の薄いオレンジ色の棒の部分は無くなったと考えてください。
切った左側のオレンジ色の棒は反力で押されていますが、もちろん右側に飛んでいくことはありません。
なぜなら、仮想断面に力が働いていてつり合いが取れているので動くことができないのです。
つまり、仮想断面に対して左方向に反力と同じ大きさの力が働いていることになります↓

この考え方でいくと内力は、AC区間内でしたらどこの位置でも、向きに注意すると-ですね。
つまり、AC区間の伸び縮み量
AC区間に生じる内力にマイナスを付けることを忘れないようにしましょう。
次に、CB区間も考えていきます。
CB区間の好きなところを切るとこんな感じですね↓

先ほどと同様に、点線のオレンジ部分は無いものと考えてください。
仮想断面に生じる内力を考えると、↓のような図になります。

今回の仮想断面には、↑の図の通り、-と
の内力が働いていますね。
つまり、CB区間の伸び縮み量
これで、仮想断面に生じる内力の考え方はおしまいです。
不静定問題を解く時のステップ④:伸び縮みした量について等式を立てる
ステップ③までできたなら、ステップ④は簡単です。
AC区間の伸び縮み量と、
CB区間の伸び縮み量の合計は0になるという式を立てましょう。
つまり、それぞれに式を代入すると、
式(2)を解くと、AEは約分できるので、
式(1)に =
を代入すると、
これで問題終了です。
いかがだったでしょうか?理解できましたか?
材料力学の不静定問題まとめ
材料力学の不静定問題の解き方はマスターできたでしょうか?
もう一度重要事項をまとめておきますと、、、
②区間ACと区間CBの伸び縮みした量を考える
③仮想的な断面に生じる内力を考える
④伸び縮みした量について等式を立てる
この4つの順番通りにすれば必ず解けます。
あと、必ず自力で図示ができるようにしましょう!
また材料力学を勉強する上でおすすめの参考書を2冊ご用意しました。
「マンガでわかる材料力学」は、kindleバージョンもあって個人的におすすめ。iPadとの相性も◎
こちらは材料力学のテスト勉強に最適です
☆ iPadがある大学生活のメリット10選はこちらの記事よりどうぞ
iphoneとiPadの2台持ちが超便利な理由10選!【iPadを5年以上使っています】
材料力学のはりの問題についても解説をまとめてあります。よろしければこちらもご覧ください。
また、解説してほしい材料力学の問題がありましたらFollow @OribiStudyのDMでご連絡ください。ありがとうございました。





