この記事を読んでくれているあなたは、
◆材料力学が苦手。
◆はりの等分布荷重の問題の解き方が分からない。
◆SFD、BMDが書けない。
という悩みを抱えていませんか?
この記事では、最も基本的な等分布荷重の問題が20分でマスターできるように丁寧な解説を作りました。
それでは頑張って材料力学の勉強をしていきましょう。
ちなみに今回解説する問題は、教科書「改訂新版 図解でわかるはじめての材料力学」の演習問題です。
YouTubeでも解説動画ありますのでぜひ。
材料力学のはりの問題って?
材料力学で頻出のはりの問題って、片持ち梁や両端支持梁、集中荷重や分布荷重など様々な種類があって難しいですよね。
この記事では、片持ち梁の等分布荷重の問題に焦点を当てて解説を作りました。
材料力学のはりの解き方(等分布荷重)

今回は、↑のような等分布荷重がかかる片持ち梁の問題の解き方をステップ毎に解説していきます。
そもそも等分布荷重[N/m]とは、↑の図の黄色の長方形で表していて、直方体で一様な重さのおもりだと認識してください。
の単位は[N/m]なので、横方向に1mで区切るとちょうど黄色のおもりの重量は1[N]であることを表しています。
今回も集中荷重の時と同様、初めに4つの重要ポイントにまとめました。この4つの手順に従って解説していきます。
①板の左端を原点として、右向き正の軸[m]をとる
②刀で板を切って仮想的な断面を作る
③等分布荷重を集中荷重に置き換える
④仮想的な断面の✖印にかかる力とモーメントを考える
この4ステップの順番通りにすれば、はりの等分布荷重の問題は必ず解けます。 それでは、実際に考えていきましょう!
はりの等分布荷重を解く時のステップ①:右向き正の 軸[m]をとる
軸[m]をとる
まずは、板の左端を原点として、右向き正の軸[m]をとりましょう。
※板の右端を原点として、左向きを正としても解けるには解けますが、考えにくいので右向き正をおすすめします。
はりの等分布荷重を解く時のステップ②:刀で板を切って仮想的な断面を作る
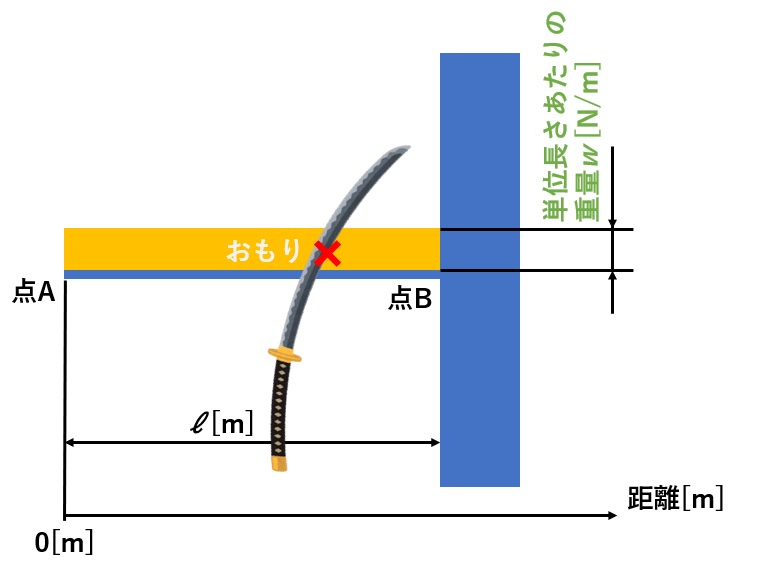
集中荷重の解き方とは異なり、今回は場合分けをする必要がないので点A~点Bのどの板の部分を刀で切っても構いません。
好きな板の部分を刀で切ると、↓のような図になりますね。
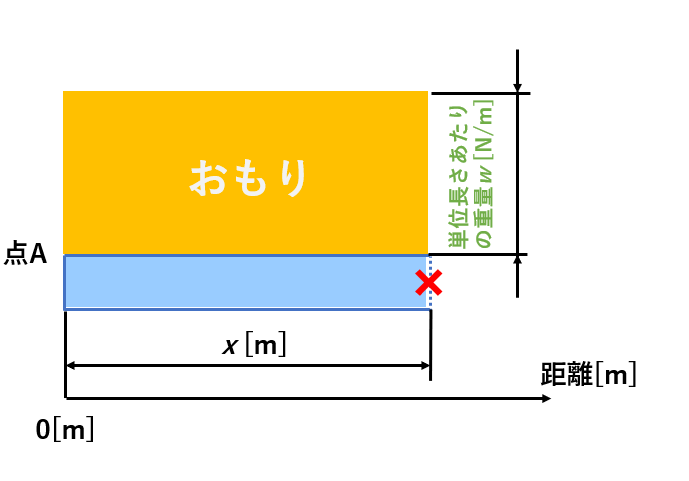
刀で板を切るところまでは理解できたでしょうか?
続いて等分布荷重で最も肝心な、等分布荷重を集中荷重に置き換えるという内容のステップに入ります。
はりの等分布荷重を解く時のステップ③:等分布荷重を集中荷重に置き換える
等分布荷重のはりの問題を解くにあたって最重要事項を書きます。必ず覚えておいてほしい注意事項です。
等分布荷重は集中荷重に変換して解く!
等分布荷重を積分使えば集中荷重に変換しないでも解けますが、手順が多く間違えやすいのでお勧めしません。
必ず等分布荷重を集中荷重に変換して考えていきましょう。
では、実際に集中荷重への変換を説明します。
初めに、変換のためのルールを説明すると、、、
おもりの全重量(×長さ)が、板のど真ん中に集中荷重としてかかっていると考える!
この変換ルールさえ覚えておけば全て簡単に解くことができます。
変換のルールを適用した図がこちらになります↓
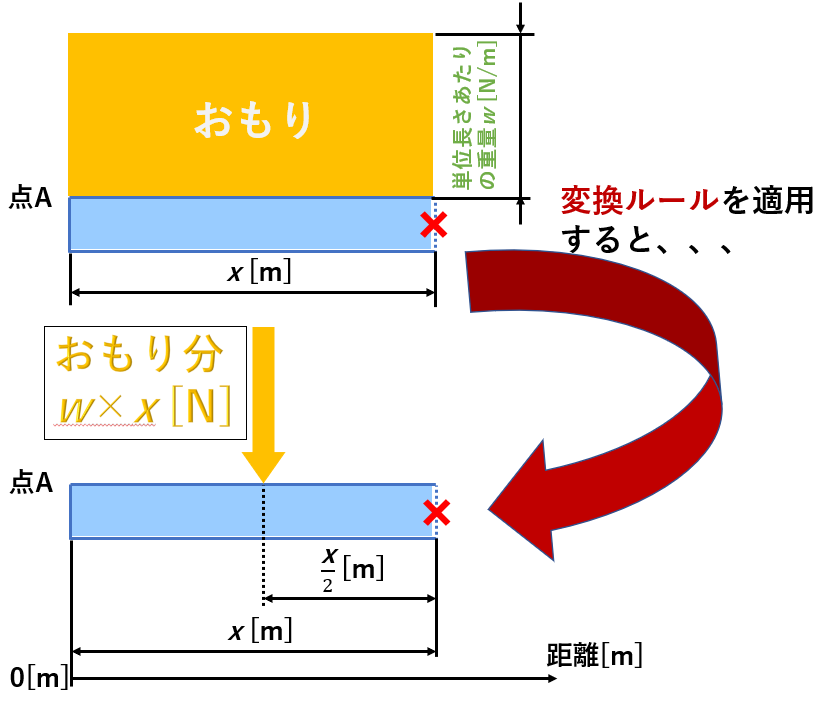
黄色の四角いおもりが黄色の矢印に変換されたのは理解できたでしょうか?
この等分布荷重(黄色の矢印)の重量は、「×長さ」で表され、ちょうど板のど真ん中の位置であることに注意してください。
ここまで理解できればあとは簡単です。
はりの等分布荷重を解く時のステップ④:仮想的な断面の✖印にかかる力とモーメントを考える
ここからは前回の集中荷重と解き方は全く同じですので、ササっと解説していきます。詰まってしまった方は、ぜひこちらから復習してみてください。
仮想的な断面の✖印にかかる力とモーメントを考えます。図示するとこんな感じです↓
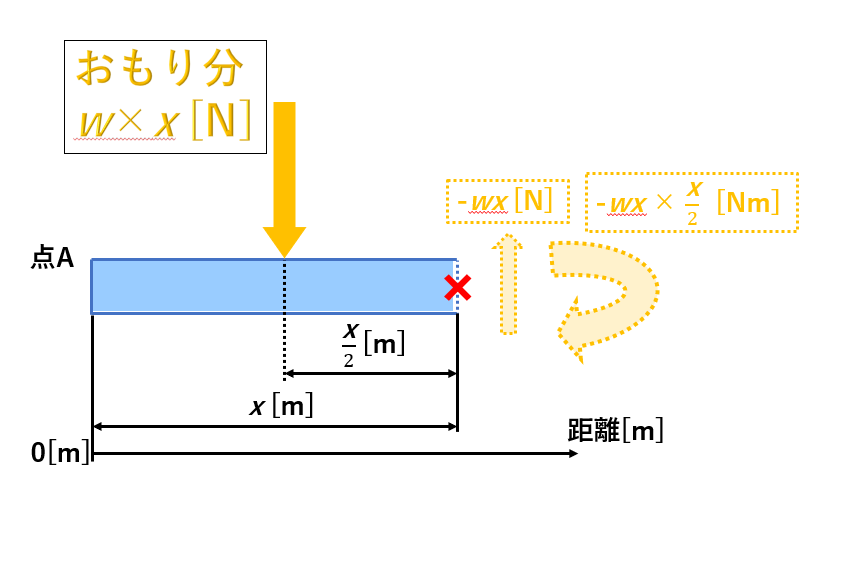
ここまでで使った式をまとめると、、、
せん断力 =
[N] ・・・(1)
曲げモーメント =
×
=
[Nm] ・・・(2)
仮想的な断面の✖印にかかるモーメントを求めるとき、うでの長さは [m]になることに気を付けましょう。
うでの長さは [m]ではありませんよ。
ここまでは理解できたでしょうか?
続いて等分布荷重のSFDとBMDを書いていきます。
もしも、SFD・BMDとはなんぞやとなった方はこちらから復習しましょう。
材料力学のはりの問題のメイン:等分布荷重のSFDとBMDグラフを書こう!
等分布荷重のSFDのグラフの書き方
SFDのグラフを書く時のポイントをもう一度まとめました。
・横軸は原点からの距離[m]
・縦軸はせん断力[N] (上向き正)

↑のグラフの赤線がSFDのグラフです。
傾きがの1次関数になります。
では、続いてBMDも書いていきましょう。
等分布荷重のBMDのグラフの書き方
横軸は原点からの距離、縦軸は曲げモーメントとしてください。
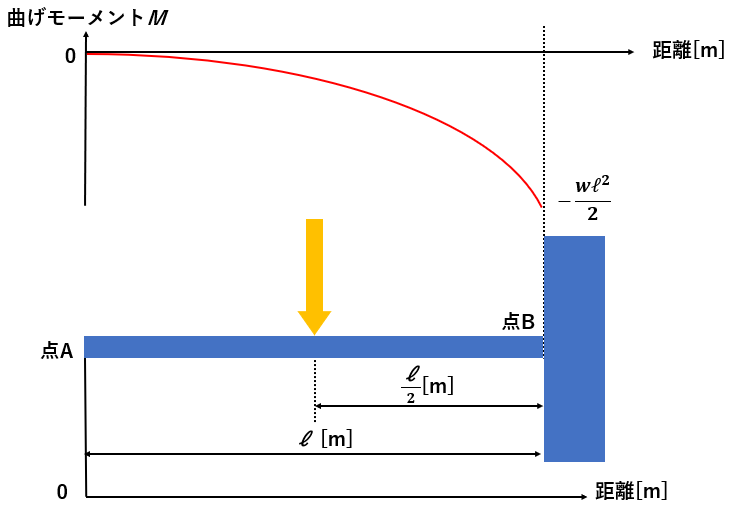
BMDのグラフは↑のような二次関数になります。
※余談ですが、このグラフから =
のとき、曲げモーメント
の大きさは最大値になることが分かるので、片持ち梁の根元部分に一番モーメントがかかっていることが分かりましたね。
つまり、片持ち梁の根元部分が一番折れやすいということを表しています。
材料力学のはりの問題まとめ
いかがだったでしょうか?
材料力学のはりの等分布荷重の問題は理解できたでしょうか?
是非何度も復習してください。
また材料力学を勉強する上でおすすめの参考書を2冊ご用意しました。
「マンガでわかる材料力学」は、kindleバージョンもあって個人的におすすめ。iPadとの相性も◎
こちらは材料力学のテスト勉強に最適です
☆ iPadがある大学生活のメリット10選はこちらの記事よりどうぞ
iphoneとiPadの2台持ちが超便利な理由10選!【iPadを5年以上使っています】
等分布荷重以外にも、材料力学のほとんどの範囲の問題解説を行っています。
また、解説してほしい材料力学の問題がありましたらFollow @OribiStudyのDMでご連絡ください。ありがとうございました。





