おりびのブログ

「機械工or院卒→開発部」を目指す理系のためのブログ。

機械工学科

材料力学の問題解説

研究室

買ってよかった物

【材料力学】熱応力の不静定問題を初心者でも解けるよう丁寧に解説！

材料力学の解説

この記事を読んでくれているあなたは、

◆材料力学が苦手。

◆不静定問題の解き方が分からない。

◆熱応力ってなに。

という疑問を抱えていませんか？

この記事では、熱応力の不静定問題が20分でマスターできるように丁寧な解説を作りました。

それでは頑張って材料力学の勉強をしていきましょう。

ちなみに今回解説する問題は、教科書「改訂新版図解でわかるはじめての材料力学」のp.48の演習問題です。

　

　

YouTubeでも解説動画ありますのでぜひ。

材料力学の熱応力の不静定問題って？
材料力学の不静定問題の解き方(熱応力)
材料力学の熱応力まとめ

材料力学の熱応力の不静定問題って？

材料の温度を上げると、物体は膨張するというのはイメージつくでしょうか？

その反対で、材料を冷やすと物体は収縮するというのはイメージできますか？

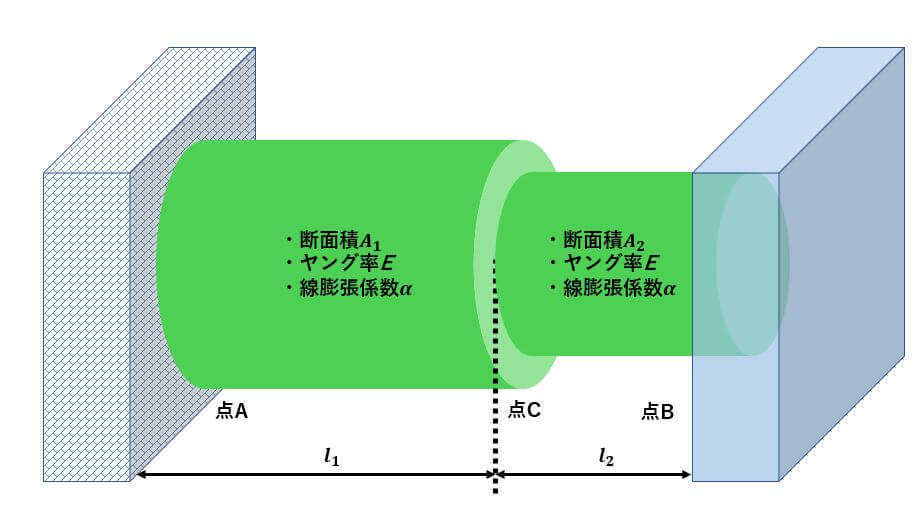
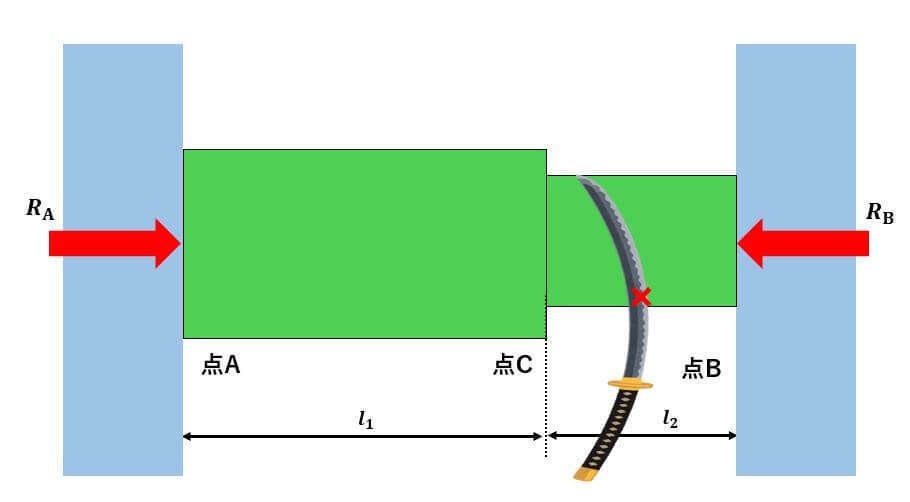
材料力学不静定問題,材料力学熱応力

今回は↑のような段付き棒が剛体壁に無理なく固定されている場合を考えます。

(※復習ですが、剛体壁＝動かない壁なので押されたとしても壁の位置は全く変わりません。)

材料力学不静定問題,材料力学熱応力

今回は、この段付き棒の温度を $t°$ 上昇させた場合のAC区間とBC区間に生じる応力 $\sigma_1$ と応力 $\sigma_{2}$ を求めます。

材料力学の不静定問題の解き方(熱応力)

温度変化によって応力が発生する場合のほとんどは不静定問題になります。

不静定問題とは？という方は先にこちらから復習しましょう。

熱応力の不静定の問題を解くにあたり重要な手順を５つにまとめました。

このステップ毎にゆっくりと理解していきましょう。

重要ポイント
①剛体壁がない場合、どのくらい伸びるかを考える
②力のつり合い式を立てる

③区間ごとに仮想断面を考えて内力を考える

④伸び縮み量を考える

⑤方程式を解く

材料力学の熱応力の解き方①：剛体壁がない場合、どのくらい伸びるかを考える

物体を熱すると膨張しますが、剛体壁がない場合どのくらい伸びるかを考えましょう。

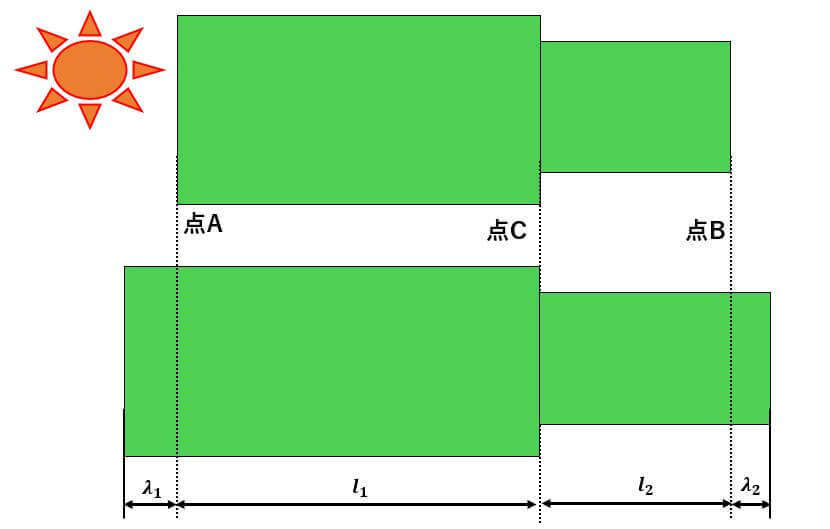
材料力学不静定問題,材料力学熱応力

もし剛体棒がない場合は↑のような図になります。

つまり、熱によって太い棒は $\lambda_{1}$ だけ伸びます。

同様に、熱によって細い棒は $\lambda_{2}$ だけ伸びます。

では、具体的に $\lambda_1$ と $\lambda_2$ を求めましょう。

$\lambda=長さ×線膨張係数×温度変化$

なので、

$\lambda_1 = l_1× \alpha× t$

$\lambda_2 = l_2× \alpha× t$

ステップ①では分かりやすくするために剛体壁がない場合どのくらい伸びるかを考えましたが、続いてステップ②では剛体壁がある場合を考えます。

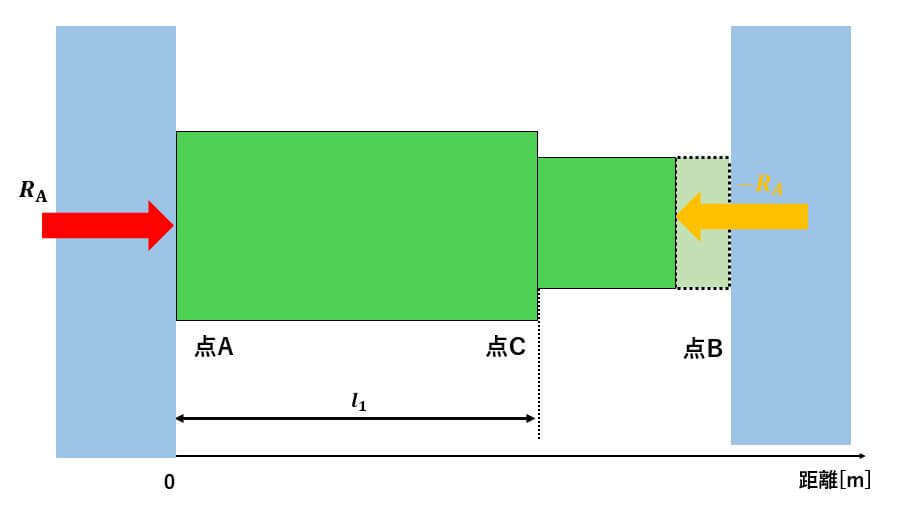
材料力学の熱応力の解き方②：力のつり合い式を立てる

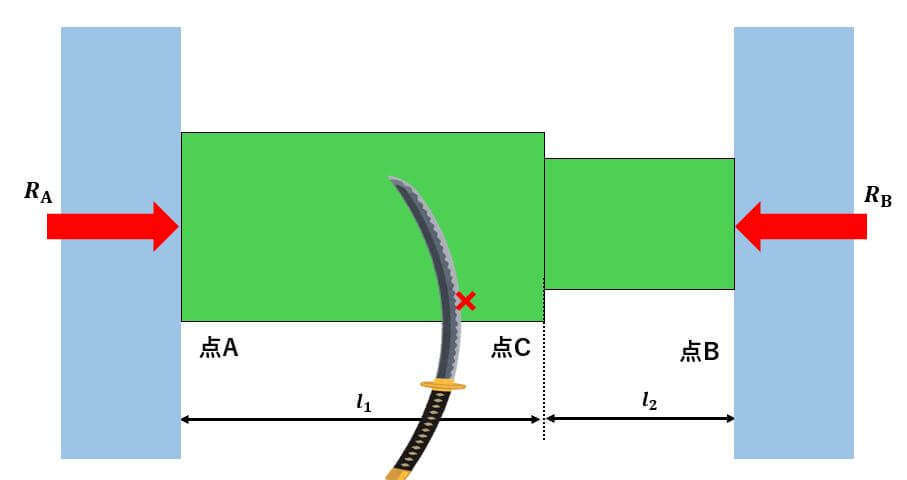
ステップ②では、剛体壁がある場合、どのような力が作用しているかを考え、力のつり合い式を立てます。熱により、段付き棒が膨張した場合、両壁に反力 $R_A$ と $R_B$ が発生するため、↓のような図になります。

材料力学不静定問題,材料力学熱応力

よって、力のつり合い式は以下のようになります。

力のつり合い式

$R_A - R_B = 0 ・・・(1)$

続いてステップ③では、仮想断面に生じる内力を求めましょう！

仮想断面に生じる内力は、不静定問題の一番の肝である伸び縮み量を求める時に必要になります。

材料力学の熱応力の解き方③：区間ごとに仮想断面を考えて内力を考える

それでは、仮想断面に生じる内力を考えましょう！

内力を求めるための重要なステップをまずはおさらいしましょう。

内力を考える時の重要ポイント

◆刀で好きなところを切る

◆切った棒の右側はないものと考える

◆仮想断面にどんな力が働いているか考える

まずは区間ACを考えます。AC区間の好きな部分を刀で切ると↓のような図になりますね。

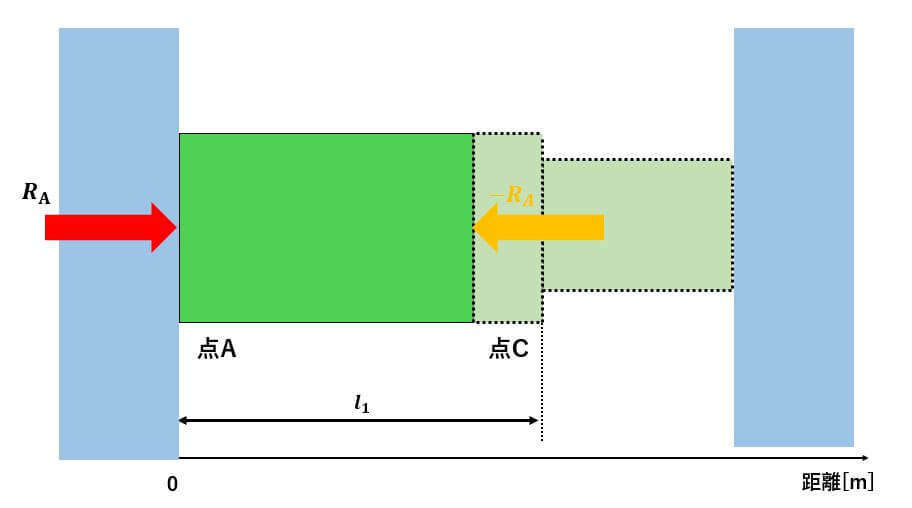材料力学不静定問題,材料力学熱応力

材料力学不静定問題,材料力学熱応力薄い緑色の点線部分は無いものと考えてください。

しかし、点線部分がないにもかかわらず緑色の物体が右方向に飛んでいかないのはなぜでしょう？

それは、仮想断面に内力 $-R_A$ が生じているからです。黄色の矢印は赤色の矢印と同じ大きさの力だけど反対向きということに気を付けてください。

同様に考えて、区間BCに働く内力を考えましょう。

まずは、区間BCの好きなところを刀で切りましょう↓

材料力学不静定問題,材料力学熱応力

区間BCに働く内力は、↓の図のように $-R_A$ です。材料力学不静定問題,材料力学熱応力

皆さん、合っていたでしょうか？

続いて最重要ポイントであり、最も難しい内容である伸び縮み量を考えましょう。

材料力学の熱応力の解き方④：伸び縮み量を考える

伸び縮み量 $\lambda$ の復習をまずはしましょう。

$\lambda = \displaystyle \frac{内力×長さ}{断面積×ヤング率}$

ヤング率 $E$ は材料固有の値なのでただの定数です。

今回注意すべきは断面積です。

区間ACの断面積は $A_1$ 、区間BCの断面積は $A_2$ ということに注意しましょう。

それではまずは、区間ACの伸び縮み量 $\lambda_1$ を求めましょう。

区間ACの伸び縮み量 $\lambda_1 = \displaystyle \frac{-R_A×l_1}{A_1×E}$

同様に区間BCは、

区間BCの伸び縮み量 $\lambda_2 = \displaystyle \frac{-R_A×l_2}{A_2×E}$

つまり、区間ACと区間BCの伸び縮み量 $\lambda$ は合わせて、

$\lambda = \lambda_1 +\lambda_2$

$=\displaystyle \frac{-R_A×l_1}{A_1×E}+ \displaystyle \frac{-R_A×l_2}{A_2×E} ・・・(2)$

ただ、ステップ①で熱による膨張した伸びの量は以下の式のように表されていました。

$\lambda = \lambda_1 + \lambda_2 = l_1× \alpha× t + l_2× \alpha× t$

つまり式を $\alpha と l$ でまとめると、

$\lambda = \alpha t( l_1 + l_2) ・・・(3)$

式(2)と式(3)が表している伸びは大きさが同じということがピンときたでしょうか？

続いて、最終ステップです。方程式を解きましょう。

材料力学の熱応力の解き方⑤：方程式を解く

式(2)は、もし剛体壁がなければ伸びていた量を表していますね。

式(3)は、剛体壁があることにより段付き棒を押し縮めた量になりますね。

伸びた・縮んだは逆ですが、変形の大きさは同じということが分かると思います。(壁が動いていないので、、、)

ですので次のような式が立ちます。

$\alpha t( l_1 + l_2) + \displaystyle \frac{-R_A×l_1}{A_1×E}+ \displaystyle \frac{-R_A×l_2}{A_2×E} = 0$

あるいは、それぞれの伸び縮み量の絶対値を考えて、

$\alpha t( l_1 + l_2) = \displaystyle \frac{R_A×l_1}{A_1×E}+ \displaystyle \frac{R_A×l_2}{A_2×E}$

でもOKです！

この式を $R_A$ について解くと、

$R_A = \displaystyle \frac{A_1 A_2 E \alpha t (l_1 + l_2)}{A_1 l_2 + A_2 l_1}$

したがって、応力 $\sigma_1$ と $\sigma_{2}$ は次のようになります。

$\sigma_1 = \displaystyle \frac{R_A}{A_1} =\displaystyle \frac{A_2 E \alpha t (l_1 + l_2)}{A_1 l_2 + A_2 l_1}$ $\sigma_2 = \displaystyle \frac{R_A}{A_2} =\displaystyle \frac{A_1 E \alpha t (l_1 + l_2)}{A_1 l_2 + A_2 l_1}$

応力 $\sigma_1$ と $\sigma_{2}$ はどちらも圧縮の応力ですね。

ここまで理解できたでしょうか？

　　　

材料力学の熱応力まとめ

材料力学不静定問題,材料力学熱応力

材料力学の熱応力の不静定問題はマスターできたでしょうか？

もう一度重要事項をまとめますと、

重要ポイント
①剛体壁がない場合、どのくらい伸びるかを考える
②力のつり合い式を立てる

③区間ごとに仮想断面を考えて内力を考える

④伸び縮み量を考える

⑤方程式を解く

この５つのステップ通り考えれば必ず熱応力の問題は解けます。

５つのステップを理解したらあとは演習あるのみです。何度も何度も問題を解いて復習していきましょう！

　　　

また材料力学を勉強する上でおすすめの参考書を2冊ご用意しました。

「マンガでわかる材料力学」は、kindleバージョンもあって個人的におすすめ。iPadとの相性も◎

マンガでわかる材料力学

末益博志, 長嶋利夫【著】オーム社出版マンガシリーズに材料力学が登場！変形や強度を考えてみよう！

　こちらは材料力学のテスト勉強に最適です

演習材料力学 (セミナーライブラリー機械工学)

尾田十八, 三好俊郎【著】サイエンス社出版大学のテスト勉強に最適！

☆ iPadがある大学生活のメリット10選はこちらの記事よりどうぞ

iphoneとiPadの2台持ちが超便利な理由10選！【iPadを5年以上使っています】

　　　　　　

　　

材料力学のはりなどの問題についても解説をまとめてあります。よろしければこちらもご覧ください。

合わせて読みたい！

また、解説してほしい材料力学の問題がありましたらFollow @OribiStudyのDMでご連絡ください。ありがとうございました。

機械工のあなたにおすすめの記事

　

おりびのブログはリンクフリーです

当サイトは管理人の許可なくリンクを張って頂いて問題ございません。
内容をコピー、スクリーンショットや画像のご利用も、該当記事へ「出典」としてリンクを張っていただければ問題ございません。
おりびのブログのホーム画面に戻る