この記事は、
◆材料力学が苦手で嫌い。
◆材料力学の演習で「ピン接合」という言葉が出てきた。
◆結局、応力が求まらない。
という方向けの記事です。
ちなみに今回解説する問題は、教科書「改訂新版 図解でわかるはじめての材料力学」ののp.31の演習問題6⃣です。

材料力学の応力に関する問題
今回は↓のような剛体棒がピン接合されている問題を解説します。
問題文は以下です。
↓の図のように、剛体棒の一端Aが剛体壁にピン接合され、途中の点CとDにおいて剛体天井に棒1(長さ、断面積
、ヤング率
)と、棒2(長さ
、断面積
、ヤング率
)とで支えられている。この剛体棒の一端Bに下向きの荷重
が作用するとき、棒1および2に生じる応力を求めよ。

↑の問題文を立体的に見ると次のようになります。
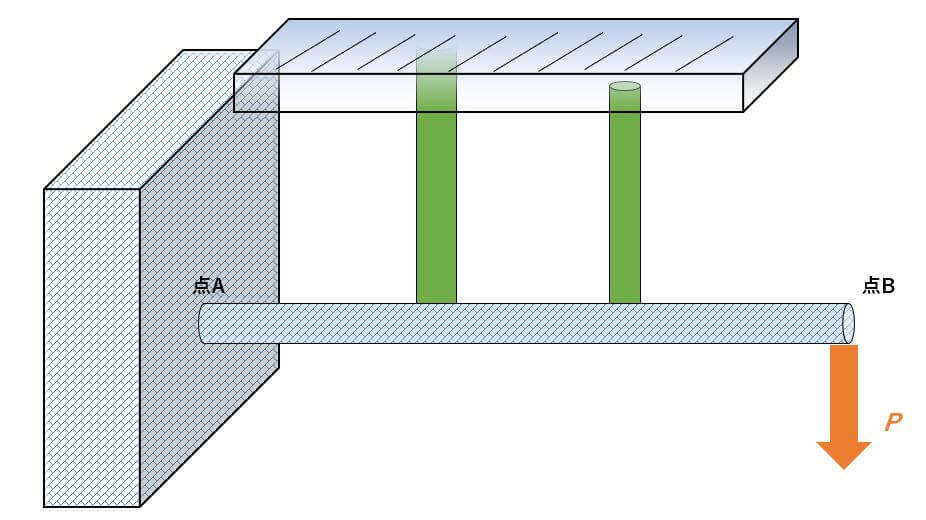
ちなみに、↑の問題文で登場した「剛体棒」という言葉と「ピン接合」という言葉の意味は分かるでしょうか?問題を解き進める前に、まずはこの2語について知っておきましょう。
★剛体棒=絶対壊れない頑丈な棒
★ピン接合=回転のみするような固定方法
この2点を覚えておきましょう。
「剛体棒」や「剛体壁」というような言葉についている剛体とは、"絶対に破壊されない頑丈な"という意味があるため剛体棒の変形は考えなくていいよという意味です。
また、ピン接合とは、↓の図のように固定はされているけど回転だけするというような構造のことです。

https://twitter.com/search?q=%E3%83%94%E3%83%B3%E6%8E%A5%E5%90%88&src=typd
つまり、ピン接合という単語を見たらモーメントが発生すると思ってください。
それでは頑張って材料力学の勉強をしていきましょう。
材料力学のせん断応力の問題を解く4つのステップ
それでは、ピンの問題を解くための重要ステップを説明します。
②モーメントのつり合い式を立てる
③伸びを求める
④代入して計算する
この4つの手順に従って解説していきます。
材料力学の問題の解き方①:力のつり合い式を立てる
棒1および2に生じる応力を求めるためには、棒1および2に生じる反力を求めることができたら簡単に解けます。(断面積は与えてくれているので。)
そこでまずは力のつり合いを考えます。
力のつり合い式を立てるために反力 、
と
を図示しましょう。↓
ポイントは、点Aにかかる反力を忘れないことです。

それでは実際に力のつり合い式を立ててみましょう。
上向きの力を正とすると、、、
ステップ①は以上です。次のステップ②ではモーメントについて考えます。
材料力学の問題の解き方②:モーメントのつり合い式を立てる
高校物理の復習ですが、モーメントとは「力×距離」でしたね。
問題は、どこの点周りのモーメントを考えるかです。
点A、点B、棒1が接している点、棒2が接している点の4つが候補として考えられます。
結論を先言うと、点A周りのモーメントを考えましょう。
点A以外だと、求めたい反力 、
や力
が消えてしまいますのでよくないです。
それでは、反時計回りを正として点A周りのモーメントのつり合い式を立てると、、、
モーメントの式はこんな感じになります。
ちなみに今回の問題では変数(求めたい値)が3つ出てきました。しかし、ステップ①と②で合わせて2つしか式がありませんよね。
ですのでもう1つ式を作らなければいけません。
ステップ③では伸びた量について考え、3本目の式を立てましょう。
材料力学の問題の解き方③:伸びを求める
今から、棒1と棒2の伸びた量をそれぞれ求めていきます。
棒1の伸びた量を、棒2の伸びた量を
としましょう。
伸びた量を求める公式を覚えているでしょうか?
↓
↓
※「長さ」は元の棒の長さのことを言います。変形後の長さではありませんよ。注意してください。
もし↑の伸びの式があまりよくわからない場合は先にこちらから復習しましょう。
では、と
を求めていきましょう。
と
を求めるのは比較的簡単だったと思います。
ポイントは次です。と
の関係式を立てていきましょう。
結論を先言うと、↓の式が成り立ちます。
先ほどのと
の値を結果を↑の比例式に代入すると、、、
そして、について整理すると、
これで、ステップ③の式変形は以上です。
なぜ の比例式が成り立つかを説明します。
初めは↓のような形をしていますが、力が加わると棒が下側に傾きます。


その時に↑の図で注目してほしいのは伸びと伸び
と点線で書かれた部分です。
棒1よりも棒2の方がより遠くにあるため大きいモーメントがかかり、伸びよりも伸び
の方が大きくなります。
つまり、伸びと伸び
の値の比は、長さ
に比例するというわけです。
理解できたでしょうか?
最終ステップは簡単です。あとはごりごり計算していくだけです。
材料力学の問題の解き方④:代入して計算する
先ほど計算した を、
モーメントの式に代入しましょう。
よって、
あとは何も考えず反力について整理していきましょう。
途中式は省略しました。ぜひ一度自分の手を動かして計算してみてください。
同様に反力を計算すると、、、
したがって棒1と棒2に生じる応力と
は反力を断面積で割ればいいので、
答えは、
となります。できたでしょうか?
材料力学の応力の問題まとめ

今回は材料力学の演習問題の中でも棒の変形とピン接合に注意する問題を解説しました。
最後にポイントを2つおさらいしておきましょう。
★点A周りのモーメントを考える
★
この2つの内容をしっかりと頭の中に入れていたら正解できるでしょう!
また材料力学を勉強する上でおすすめの参考書を2冊ご用意しました。
「マンガでわかる材料力学」は、kindleバージョンもあって個人的におすすめ。iPadとの相性も◎
こちらは材料力学のテスト勉強に最適です
☆ iPadがある大学生活のメリット10選はこちらの記事よりどうぞ
iphoneとiPadの2台持ちが超便利な理由10選!【iPadを5年以上使っています】
また、他の材料力学の問題もたくさん解説しています。
不静定問題やはりの問題なども見てみたいという方はこちらからどうぞ!↓
また、解説してほしい材料力学の問題がありましたらFollow @OribiStudyのDMでご連絡ください。ありがとうございました。





