この記事は、
◆材料力学が苦手。
◆不静定問題の解き方が分からない。
というあなた向けの内容です。
材料力学の不静定問題が初心者でも解けるよう、3DCADなどを用いた分かりやすい図解を多く使って解説しています、ぜひご覧ください。
ちなみに今回解説する問題は、教科書「改訂新版 図解でわかるはじめての材料力学」のp.48の演習問題です。
YouTubeでも解説動画ありますのでぜひ。 youtu.be
材料力学の不静定問題って?
不静定問題は材料力学の王様と言っていいほど頻出で重要な内容です。
しかし、力の向きが分かりにくかったり、そもそも引張りなのか圧縮なのか分かりにくいという場合がありますよね。
本記事では図解多めで丁寧に解説しています。ぜひ最後までご覧ください。
ボルトとナットを使った典型的な材料力学の不静定問題
今日はボルトとナットを使った典型的な材料力学の不静定問題の解説をします。

正直僕は、初めて教科書でこの問題を見た時、ボルトとナットと中空円筒にどのような力が働いているかすらイメージできませんでした。
そこで、初心者でも分かるように、分かりやすい立体の図形を作りました。
まずは↓のボルトとナットだけの立体図をご覧ください。

そして、このボルトとナットの間に真鍮製の中空円筒を無理なく挟みました。(※この時点で応力は発生していないという意味です。)

細かい寸法や材料特性をまとめた図が↓になります。
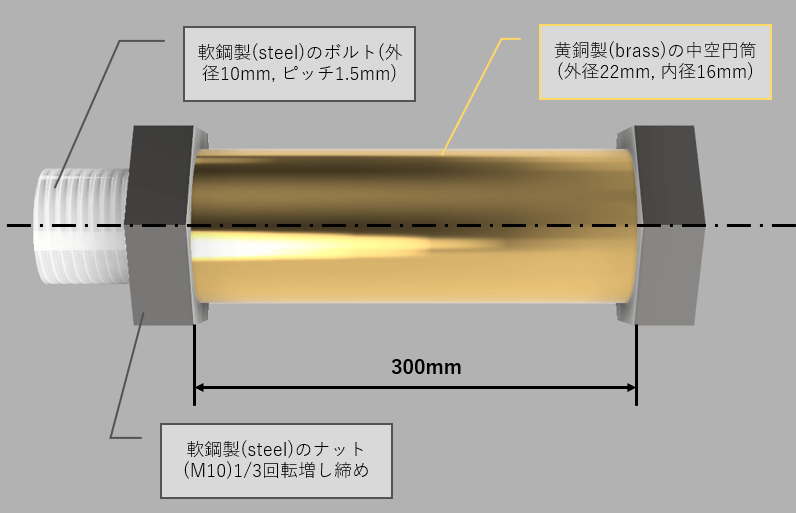
今回の記事では、ナットを1/3回転増し締めしたときにボルトに生じる応力と中空円筒に生じる
を求めましょう。
※軟鋼はsteel、真鍮はbrassなので頭文字をとってsとbを付けています。
ナットとボルトと中空円筒の不静定問題を解くステップは4つしかありません。
この4ステップ通り進めれば必ず解けます。まずは重要ポイントを4つ説明します。
②反力を仮定し、力のつり合い式を立てる
③ボルトの伸び量と中空円筒の縮み量を求める
④伸び縮みした量について等式を立てる
それでは材料力学を勉強していきましょう。
不静定問題を解くためのステップ①:かかる力をイメージするために絵を書く

早速ですが、中空円筒を無理なく挟んだ絵と、もし中空円筒がなかったらどうなっているかを絵で表しました。
ピッチmmのナットを1/3回転させたので、もし中空円筒がなければ
だけナットが移動したことになりますね!
しかし、中空円筒があるために突っかかって実際はも進むことができません。
ここまではイメージできましたでしょうか?
続いて、中空円筒がある場合の絵を↓の表します。

この↑の図の注目ポイントを箇条書きで書きます。
◆ナットは よりも進む量が少ない
◆ボルトが元よりも 伸びた
◆中空円筒は元よりも 縮んだ
ステップ①では上の3つの注目ポイントが理解できればOKです!
続いてステップ②で力のつり合い式を立てましょう。
不静定問題を解くためのステップ②:反力を仮定し、力のつり合い式を立てる
中空円筒は押しつぶされるような力が働くので、ナットの進む向きと反対方向の左向きに反力を仮定しました。
ボルトには、引っ張られるような、引き伸ばされるような力が働くので、ボルトには左向きに反力を仮定しました。
そこで右向きを正として力のつり合い式を立てると、
ポイントは、力はボルトと中空円筒にしか働かないということです。
ナットには力が作用していないということに注意しましょう。
続いてステップ③で、ボルトの伸び量と中空円筒の縮み量を求めましょう。
不静定問題を解くためのステップ③:ボルトの伸び量と中空円筒の縮み量を求める
伸び縮み量の復習をまずはしましょう。
ヤング率は材料固有の定数で、ボルトが
で中空円筒が
です。
長さはボルトも中空円筒もmmですね。
長さとは、変形前の元の長さを表しています。変形後の長さではないので気を付けてください。
これは、縦ひずみの定義式からも理解できます↓
右辺の分母は変形後の長さではなく、変形前の長さを使います。
: 縦ひずみ、
: 変形後の棒の長さ、
: 棒の元の長さ
(※2019/08/01追記↑)
断面積は、ボルトがで中空円筒が
です。
これらに注意すると、 と
は以下のようになります。
※式(1)を式(2)に代入しています。
ここまで理解できたでしょうか?
いよいよ最終ステップです。
不静定問題を解くためのステップ④:伸び縮みした量について等式を立てる
ボルトが伸びた量と中空円筒が縮んだ量
の和が、増し締めされてナットが移動した量
と等しくなりますね。
つまり、以下のような式になります。
※伸びた量(プラスの値)と縮んだ量(負の値)の和を求めるので、式(4)は+ではなくーで表しています。
あるいは、ボルトが伸びた量の大きさ(絶対値)と中空円筒が縮んだ量
の大きさ(絶対値)がナットの増し締め量と等しくなります。
式(4)あるいは式(5)をについて解くと、以下のようになります。
式(6)からを計算すると、
なので
を計算すると、
上の式(7,8)に値を代入したらこの問題は終わりです。
GPa、
GPa、
m、
m
SI単位系に直すと↑のようになりますね!そして、次に面積と
を求めましょう。
面積は簡単に求まりますね、外径10mmなので、
少しややこしいのは面積です。
外径22mm、内径16mmの中空円筒なので、
それでは、上の式(7,8)に値を代入していきましょう。
同様に考えて、
は圧縮応力が働くため負の値のなることに気を付けましょう。
これでボルトと中空円筒の不静定問題はおしまいです。
材料力学の不静定問題まとめ

今回はボルトとナットが登場する不静定問題を解説しました。おそらくどの教科書・問題集にも載っている有名な問題だと思います。
しっかりと復習してテストで解けるようにしましょう。
また材料力学を勉強する上でおすすめの参考書を2冊ご用意しました。
「マンガでわかる材料力学」は、kindleバージョンもあって個人的におすすめ。iPadとの相性も◎
こちらは材料力学のテスト勉強に最適です
☆ iPadがある大学生活のメリット10選はこちらの記事よりどうぞ
iphoneとiPadの2台持ちが超便利な理由10選!【iPadを5年以上使っています】
また、不静定問題以外にもはりの問題なども解説しているのでよかったらそちらも勉強していってください。
また、解説してほしい材料力学の問題がありましたらFollow @OribiStudyのDMでご連絡ください。ありがとうございました。





