この記事では、
◆材料力学の試験が近くてヤバい。
◆材料力学のねじりの問題の解き方が分からない。
◆材料力学の演習・解説が見たい。
というあなた向けの内容です。
分かりやすくするために図解を多く使っています。
さっそく材料力学の勉強をスタートしていきましょう。
ちなみに今回解説する問題は、教科書「改訂新版 図解でわかるはじめての材料力学」のp.67の演習問題4⃣です。
材料力学のねじりの不静定問題
今日解説する問題はねじりに関する不静定問題です。
問題文は以下です。
下の図のように段付き丸棒を剛体壁に固定して点Cにねじりモーメントを加える時、固定端に生じるねじりモーメント
および、
を求めよ。また、点Cのねじれ角
を求めよ。ただし、せん断弾性係数を
とする。

という問題を解説していこうと思います。
材料力学のねじりの問題を解くための重要5ステップ
いつもの例のごとくまずは、ねじりの不静定問題を解くための重要ステップを5つご紹介します。
②モーメントのつり合い式を立てる
③AC区間、BC区間に発生するねじりモーメントを求める
④ねじれ角とモーメント
の関係式を思い出す
⑤ねじれ角の和が等しい
この4つの手順通り真似すれば必ず解くことができますよ!
材料力学のねじりの問題を解くためのステップ①:問題をイメージするために絵を書く
もはや、方程式を作る以前に絵を書くというのは必須な手順ですね。
↓が教科書の問題文の図ですが、皆さんイメージが湧いていいるでしょうか?少しイメージしにくくないですか?

↑の図を見て立体図が思い浮かぶようになることを目指しましょう。
問題文の立体図は↓です、よくチェックしてねじりの問題のイメージを思い浮かべてください。
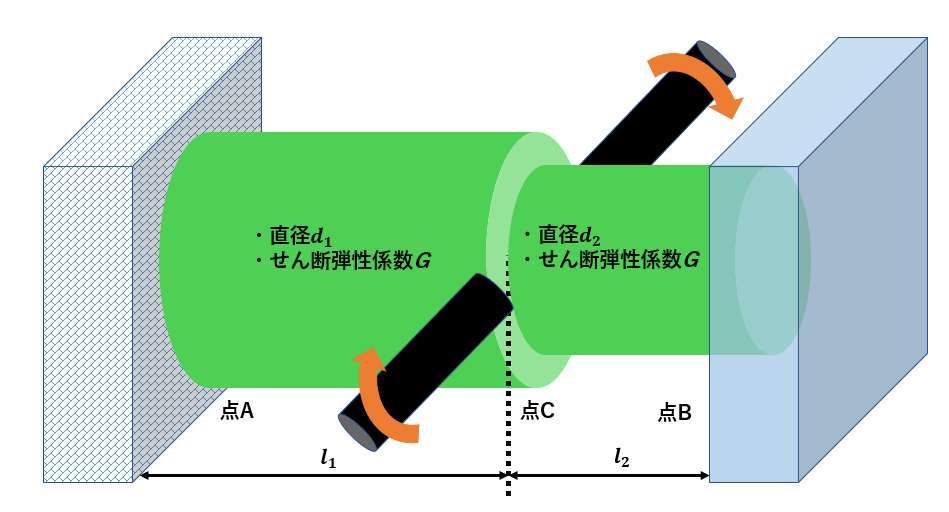
点Cの黒い棒が刺さっていて、それを時計回りに回転するようにトルクをかけているようなイメージです。
ポイントは、段付き棒の両側は剛体壁=動かない壁にひっついているので、棒がねじきれたり壊れたりしないということです。
つまり、両壁にねじりモーメントと
が発生しますね。
材料力学のねじりの問題を解くためのステップ②:モーメントのつり合い式を立てる
剛体壁の両側にモーメントが発生している図を↓に表します。

※余談ですが、ダブル矢印でモーメントを表しています。右ネジの法則より、ダブル矢印と回転方向がリンクしています。
↑の立体図を二次元図にすると↓のようになります。
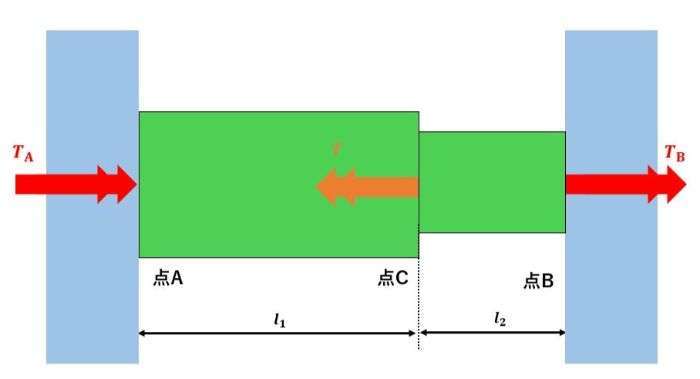
それでは、モーメントのつり合い式を立てましょう。やり方は力のつり合いとほぼ同じ考え方です。
材料力学のねじりの問題を解くためのステップ③:AC区間、BC区間に発生するねじりモーメントを求める
不静定問題を解くための準備として、AC区間、BC区間に発生するねじりモーメントを求めていきましょう。
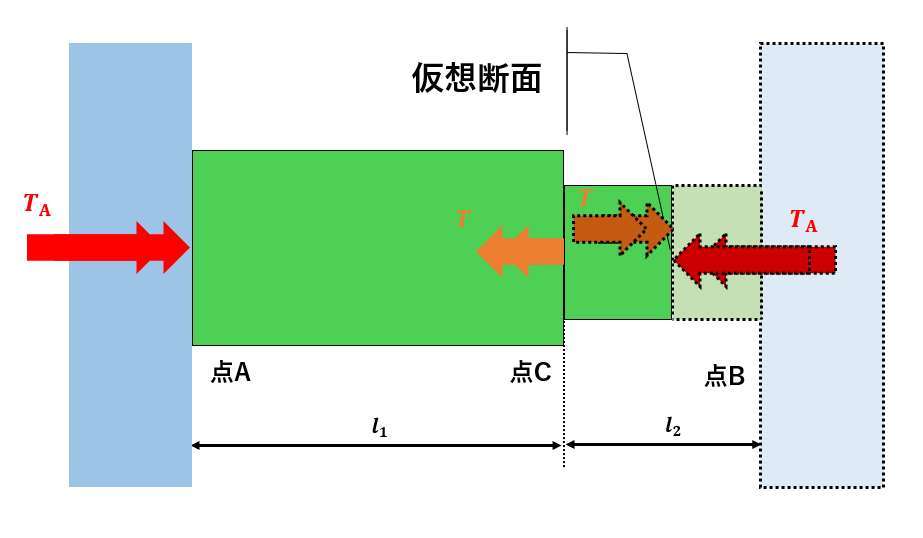
仮想断面を考えて求めていきます。
※もし仮想断面に生じるモーメントの求め方に自信がないという方は、ぜひ先にこちらから仮想断面について勉強しましょう。こちらは必読です。
ある程度仮想断面について分かっているという前提で話を進めていきますと、、、
まず、↓の図のようなAC区間に仮想断面がある場合を考えます。

いいですか、点線の部分は無いものとして考えてください。しかし緑色の部分が右に飛んでいかないのは仮想断面にと反対向きのねじりモーメントが働いているからですね。
つまり、AC区間の仮想断面に生じるねじりモーメントはですね。
(※仮想断面に生じるダブル矢印が左向きを正としました。もちろん負にしても解けます。)
同様に考えて、BC区間の仮想断面に生じるねじりモーメントを求めましょう。
↑の図の仮想断面にはと
の2つのねじりモーメントがかかっていることが分かりますね。
仮想断面に生じるダブル矢印が左方向を正とすると、BC区間の仮想断面に生じるねじりモーメントはですね。
ここまででステップ③は終了です。
続いてのステップ④では、不静定の問題を解くためにねじれ角について考えていきます!
材料力学のねじりの問題を解くためのステップ④:ねじれ角 とモーメント
とモーメント の関係式を思い出す
の関係式を思い出す
さあ、ねじれ角とモーメント
の関係式をぱっと思い出せるでしょうか?
: 半径、
: 比ねじれ角、
: ねじれ角、
: せん断弾性係数、
: ねじりモーメント、
: 断面二次極モーメント
比ねじれ角[rad/m]とねじれ角
[rad]を混同しないように気を付けましょう。
比ねじれ角は1mあたりのねじれた角度を表しているので単位は[rad/m]ですね。
結局、↑の式たちを変形して、以下の式を計算で用います。
: 直径、
: ねじれ角、
: せん断弾性係数、
: ねじりモーメント
このねじれ角 に関する式を最終ステップで使います。
必ず↑のねじれ角に関する式を導けるようにしておきましょう。
材料力学のねじりの問題を解くためのステップ⑤:ねじれ角 の和が等しい
の和が等しい
最終ステップでは、ついに方程式を立てて解いていきます。
方程式を立てるために必ず知っておいてほしい内容は以下です。
つまりAC区間のねじれ角とBC区間のねじれ角
の合計が
になるように式を立てましょう。
以下のようになります。
ねじれ角との関係式を代入して、、、
あとは、↑の式をについて解けば終わりです。
一応、解いた結果は以下のようになります。
最後に、点Cにおけるねじれ角を求めましょう。
以上で解説は終了です、皆さん理解できたでしょうか?
材料力学のねじりの不静定問題まとめ

ねじりの問題はたくさん公式が出てくるので少し戸惑いますよね、一度理解したら後は演習あるのみです。
また材料力学を勉強する上でおすすめの参考書を2冊ご用意しました。 「マンガでわかる材料力学」は、kindleバージョンもあって個人的におすすめ。iPadとの相性も◎
こちらは材料力学のテスト勉強に最適です
☆ iPadがある大学生活のメリット10選はこちらの記事よりどうぞ
iphoneとiPadの2台持ちが超便利な理由10選!【iPadを5年以上使っています】
また、不静定問題以外にもはりの問題なども解説しているのでよかったらそちらも勉強していってください。
また、解説してほしい材料力学の問題がありましたらFollow @OribiStudy
のDMでご連絡ください。ありがとうございました。





