この記事を読んでくれているあなたは、
◆材料力学が苦手。
◆材料力学の演習でピンの問題が出てきた。
◆許容応力ってなんじゃ。
という悩みを抱えていませんか?
この記事では、材料力学の問題の中でも、ピンの引張り応力とせん断応力を考える問題を丁寧に解説に解説します。
それでは頑張って材料力学の勉強をしていきましょう。
ちなみに今回解説する問題は、教科書「改訂新版 図解でわかるはじめての材料力学」のp.30の演習問題です。

材料力学のピン接合の問題?
今回は、↓のようなピンが登場する材料力学の問題で、引張り応力とせん断応力が発生する場合を考えます。
問題文は以下です。
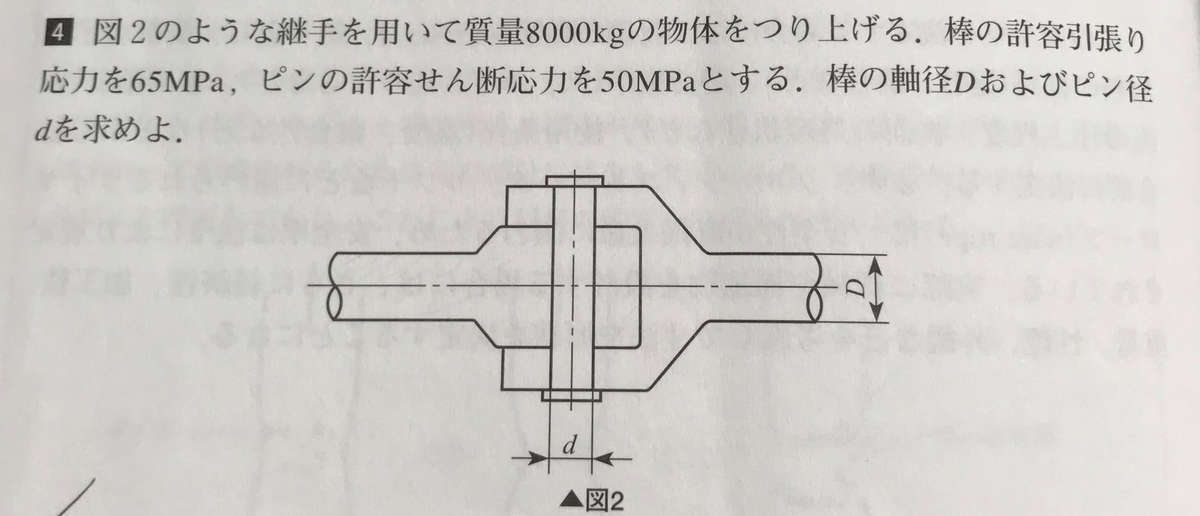
以下の図のように継ぎ手を用いて質量の物体を吊り上げる。棒の許容引張り応力
、ピンの許容せん断応力
とする。棒の軸径
およびピンの直径
を求めよ。
この問題文と図だけでは非常に難しく感じますよね。
ですのでまずは、以下の立体図をよく見て、問題のイメージを膨らませましょう。

↑のような内側に空洞があって、側面に穴があいているような黄色の継ぎ手Yがあるとします。
(※色は分かりやすくするために付けたのであまり気にしないでください。)
そして次に、側面に穴の開いた赤色の継ぎ手Rを用意します。↓

継ぎ手Yと継ぎ手Rはちょうどはめ込むことができるように作られているとしましょう。こんな感じにはまります↓

穴が開いている真正面から見ると次のようになります↓

この穴にピンを刺してみましょう。ピンの形状は以下のようです↓
ただの棒だと思ってください。

ピンを刺すと、最終的にはつぎのような絵になりますね。↓

問題文を見て、↑のような立体図を想像できるかということが重要です。
その点、教科書は2次元図面しかなくて不親切ですよね笑
では次のセクションでは、引張り応力とせん断応力の問題に分けながら
◆問題の具体的な解き方
◆許容応力とは何か
ということについてステップ毎に解説していきます。
それでは頑張って材料力学を勉強していきましょう。
材料力学のピンの問題を解く3つのステップ

それでは、ピンの問題を解くための重要ステップを説明します。
②「許容応力>棒にかかる応力」になるように式を立てる
③四捨五入に注意して答えを出す
この3つの手順に従って解説していきます。
まずは引張り応力について解こう!
「物体を吊り上げる」と問題に書いてあった訳ですから、軸径の棒には引張りの力が加わっていますね。
ではまずは簡単な棒の軸径を求めていきましょう。
材料力学のピンと継ぎ手の問題の解き方①:応力の定義式を思い出す(断面積に注意!)
まずは応力の定義式を思い出しましょう。
※もし忘れてしまったという方は、まずこちらから復習してみてください。
応力とは、応力とは、物体中の「仮想断面」に働く「内力」を仮想断面の「断面積」で割ったものです。数式で書くと次のようになります。
まずは、「仮想断面に働く断面積」ですが、これは言うまでもなくですね。
また、「仮想断面に働く内力」ですが、㎏ではないですよ。
質量は㎏と書かれていましたが力の単位であるNに変換しないといけないので
Nとなりますよ。
重力加速度であるをかけるのを忘れないでください。
よって、この棒にかかる引張り応力をとすると、
になります。
これでステップ①はおしまいです。
続いてステップ②では一番の難関である許容応力について説明していきます。
材料力学のピンと継ぎ手の問題の解き方②:「許容応力>棒にかかる応力」になるように式を立てる
まず、許容応力とはその部材にかかってもよい限界の値のことを言います。
※添え字のはallowable(許容)を表しています。
つまり許容応力はかかってもいい応力のリミットだと思ってください。
ですので必ず「許容応力>棒にかかる応力
」になることを頭に入れておいてください。
許容応力よりも実際に生じる応力
の方が大きくなるなんてことはあり得ません。
このことに気を付けると、以下のような式が導けます。
これをDについて解くと、
したがって両辺にルートを付けると、
となります。
ほぼこれで答えが出ましたが、最終ステップで引っかからないように注意しましょう。
材料力学のピンと継ぎ手の問題の解き方③:四捨五入に注意して答えを出す
先ほどの計算では棒の軸径はこのようになりましたね。↓
そこで、単純に四捨五入して、
と答えてはいけません。
正しい答えは、
になります。
単純に四捨五入すると正しい答えにならない場合があります。
今回は四捨五入ではなく、「有効数字3桁目の切り上げ」をしましょう。
ちなみに、]を
の式に代入し直してみると、
となり、許容応力を厳密には超えてしまうからです。
「許容応力」という単語が問題文中に登場したら答えは四捨五入ではなく切り上げだと頭に叩き込んでおきましょう。
これで引張り応力に関する解説は以上になります。同じような流れでせん断応力についても解説していきます!
次にせん断応力について解こう!
では続いて、ピンの軸径を求めていきましょう。
もう一度画像を見ながら説明していきます。
この黄色と赤色の継ぎ手に空いた穴にピンを刺します。


↑の状態で、赤色の継ぎ手が下に引っ張られるとピンは千切れるような力が加わります。
この時青色のピンの軸径がどのくらい太いとせん断されないかを求めていきます。
断面積に注意すれば後は簡単ですので頑張っていきましょう。
材料力学のピンと継ぎ手の問題の解き方①:応力の定義式を思い出す(断面積に注意!)
先ほども応力とは、物体中の「仮想断面」に働く「内力」を仮想断面の「断面積」で割ったものと言いました。
結論からいうと、
◆内力:N
◆断面積:
です。内力は引張り応力の時と同じです。
しかし断面積が異なり、ピンの軸の断面積の2つ分になることに気を付けてください。
↓の図で示した通り、ピンはこの2か所でせん断されるので断面積は2つ分ですね。ここに注意しましょう。

よって、この棒にかかるせん断応力をとすると、
になります。
これでステップ①はおしまいです。
材料力学のピンと継ぎ手の問題の解き方②:「許容応力>棒にかかる応力」になるように式を立てる
引張り応力の時もせん断応力の時も「許容応力>棒にかかる応力」という考え方は変わりません。
許容せん断応力をとすると、以下の式になります。
これをdについて解くと、
したがって両辺にルートを付けると、
となります。
これでステップ②は終わりです。
再び「四捨五入と切り上げ」に気を付けましょう。
材料力学のピンと継ぎ手の問題の解き方③:四捨五入に注意して答えを出す
結論からいうと答えは
になります。
今回は四捨五入でも切り上げでも同じ結果になりますが、先生によってはわざと四捨五入させる問題を作る可能性もありますので十分注意してください。
材料力学のピンと継ぎ手の問題まとめ

材料力学でピンと継ぎ手が登場する問題で気を付けるべき点は次の2点です。
◆力がかかる断面積に注意
◆許容応力が与えられた場合は「切り上げ」
この2つに注意すれば恐らく解けると思います。
テスト勉強頑張ってください。
また、解説してほしい材料力学の問題がありましたらFollow @OribiStudyのDMでご連絡ください。ありがとうございました。



