材料力学の不静定問題！よく出る不静定問題を４つのステップ毎に解説

この記事は、

◆材料力学が苦手。

◆不静定問題の解き方が分からない。

というあなた向けの内容です。

テスト前のあなた、しっかりと勉強を進めていきましょう。

材料力学不静定問題,材料力学内部応力

材料力学の不静定問題
材料力学の不静定問題を解く４つの重要ステップ
材料力学の不静定問題まとめ

材料力学の不静定問題

今回は、ちょっと変わった不静定問題の解説を行います。

丸棒が3本も登場するので少々難しく感じるかもしれません。

しかし、不静定問題は解き方はワンパターンなので、慣れてしまえば簡単です。

今日は↓のような問題を解きます。

材料力学不静定問題,材料力学内部応力

長さが $\delta$ だけ異なる3本の丸棒が上下対称に配置され、剛体壁と剛体板の間に挟まれた状態になっている。剛体板に外力 $F$ を作用させたところ、部材1の2本の丸棒が $\lambda$ だけ縮んだ状態で釣り合った。 $\lambda$ の大きさを求めよ。ただし、部材1および部材2の直径とヤング率は、( $D_1 = 8mm,E_1 = 100GPa$ )、( $D_2 = 24mm,E_2 = 200GPa$ )とする。また、部材1の元の長さは $L = 180mm$ , 部材1と部材2の長さの差は $\delta = 0.04mm$ , 外力 $F = 2000kgf$ とする。

まずは、立体図を見てイメージを膨らませましょう。

細い丸棒が2本、赤色の板に無理なく固定させています。(この時点で細い丸棒に応力はかかっていません。)

また、少し短い黄色の丸棒が板の真ん中に固定されています。

この状態で、上側の赤色の板を押して黄色の棒が縮むまで押し込みます。

こういった場合を考えています。↓

材料力学不静定問題,材料力学内部応力

この立体図を真正面から見ると↓のようになります。

材料力学不静定問題,材料力学内部応力

それでは、ステップ毎に問題を解説していきます。

材料力学の不静定問題を解く４つの重要ステップ

材料力学の内部応力を解くために、次の４つの手順に従って説明していきます。

この４ステップで必ず不静定問題は解くことができます。

重要ポイント ①反力を仮定し、力のつり合い式を立てる　
②それぞれの丸棒の縮んだ量を考える

③縮んだ量について等式を立てる

④値を代入して計算する

この４つの手順に従って解説していきます。

材料力学の内部応力の解き方①：反力を仮定し力のつり合い式を立てる

材料力学を解くにあたってお馴染みの手順です。まずは力のつり合いを考えましょう。

材料力学不静定問題,材料力学内部応力

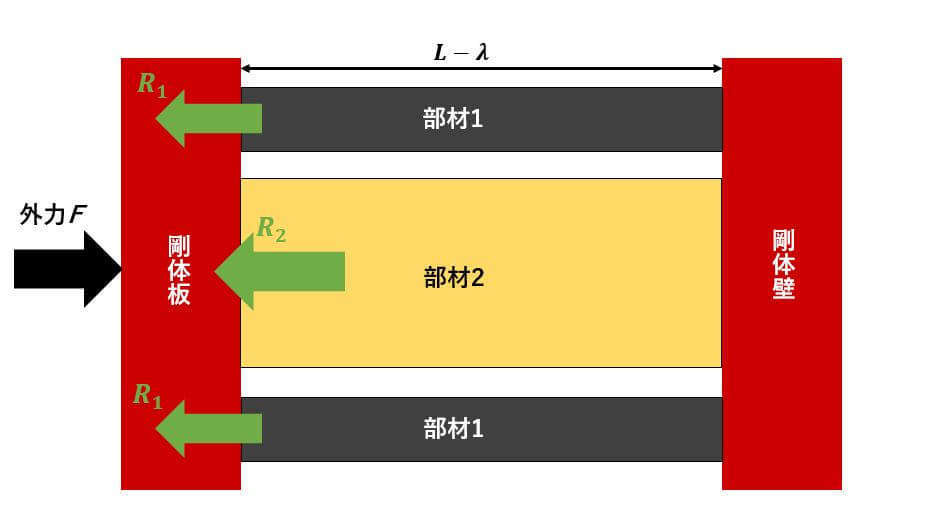
外力 $F$ に対して反発するような力が発生するので、部材1には反力 $R_1$ が、部材2には反力 $R_2$ がかかります。

よって、力のつり合い式を立てると、、、

力のつり合い式

$F-2R_1-R_2 = 0$

力のつり合い式までは立てることができたでしょうか？

余談ですが、これまでの↑の図を見て赤色の四角形が「剛体板」と「剛体壁」になっていることに気づいたでしょうか？

ちょっと重要ポイント ★「剛体」は絶対に壊れない

★剛体「壁」は動かない

★剛体「板」は動く

この違いは知っておくと戸惑いが減ります！ぜひ覚えといてください。

ステップ②ではそれぞれの部材の縮んだ量を求めていきますよ。

材料力学の内部応力の解き方②：それぞれの丸棒の縮んだ量を考える

今から、部材1と部材2の縮んだ量をそれぞれ求めていきます。

部材1の縮んだ量を $\lambda_1$ 、部材2の縮んだ量を $\lambda_2$ としましょう。

縮んだ量を求める公式を覚えているでしょうか？

↓

$\lambda = \displaystyle \frac{内力×長さ}{断面積×ヤング率}$

※「長さ」は元の棒の長さのことを言います。変形後の長さではありませんよ。注意してください。

では、 $\lambda_1$ と $\lambda_2$ を求めていきましょう。

$\lambda_1= \displaystyle \frac{-R_1 L}{A_1 E_1}$ , $\lambda_2= \displaystyle \frac{-R_2 (L-\delta)}{A_2 E_2}$

間違いやすいポイントは、 $\lambda_2$ の「長さ」です。

部材2の元の長さは $L$ ではなく $L-\delta$ です。ここだけ間違えないように注意しましょう。

次のステップでは $\lambda_1$ と $\lambda_2$ の関係式について考えていきます。

材料力学の内部応力の解き方③：縮んだ量について等式を立てる

いきなり $\lambda_1$ と $\lambda_2$ の関係式を立てるのは難しいので、まずはそれぞれの部材の変形前・変形後の長さを考えます。

もう一度図を見ながら、変形前・変形後の長さに注目してみましょう。

材料力学不静定問題,材料力学内部応力

◆部材1 : $L → L-\lambda$

◆部材2 : $L-\delta → L-\delta - (\lambda-\delta)$

では次に、変形後の長さから変形前の長さを引いて変形量を求めましょう。

↓のようになりますね。

◆部材1 : $(L-\lambda) - L =-\lambda$

◆部材2 : $L-\delta - (\lambda-\delta) - (L-\delta) = \delta-\lambda$

よって、部材1の変形量 $\lambda_1$ は $-\lambda$ と等しく、部材2の変形量 $\lambda_2$ は $\delta-\lambda$ と等しくなりますね。

なので、この通り変形量に関する式を立てると、、、

変形量に関する式

$\lambda_1=- \displaystyle \frac{R_1 L}{A_1 E_1}=-\lambda$

$\lambda_2=- \displaystyle \frac{R_2 (L-\delta)}{A_2 E_2}=\delta-\lambda$

あとはゴリゴリ $R_1$ と $R_2$ について解いていけばいいのですが、このままでは少々計算が煩雑です。

$L-\delta$ の項がかなり邪魔ですよね。もしこいつが無かったら $L$ が簡単に消えるので非常に楽です。

そこで朗報ですが、 $L-\delta\fallingdotseq L$ と近似してOKです。めっちゃ楽ですよね。

↑のように近似してもよい理由を述べます。

$L-\delta$ を $L$ で無理やりくくると、

$L-\delta=L(1-\displaystyle \frac{\delta}{L})$

そして、 $L$ は $180mm$ 、 $\delta$ は $0.04㎜$ なので、

$\displaystyle \frac{\delta}{L} = \displaystyle \frac{0.04㎜}{180㎜}=0.00022$ となりますね。

$0$ が4個も続きます。材料力学は基本、有効数字3桁ですので $0$ が4個も続く場合はほぼ $0$ とみなしてよいというわけです。

ですので近似が成立して、 $L-\delta =L(1-0.00022) \fallingdotseq L$ となります。

そうすると、反力 $R_1$ と $R_2$ は次のようになります。

$R_1= \displaystyle \frac{A_1 E_1}{L}\lambda$ , $R_2= \displaystyle \frac{A_2 E_2}{L} (\lambda -\delta)$

ここでステップ③は終わりです。

最終ステップで、値をそれぞれ代入して数値を計算しましょう。

材料力学の内部応力の解き方④：値を代入して計算する

初めに書いた力のつり合い式に反力 $R_1$ と $R_2$ を代入していきましょう。

$F-2R_1-R_2 = 0$ に $R_1$ と $R_2$ を代入すると、、、

$F - 2\displaystyle \frac{A_1 E_1}{L}\lambda - \displaystyle \frac{A_2 E_2}{L} (\lambda -\delta) = 0$

したがって、 $\lambda$ について解くと、、、

$\lambda = \displaystyle \frac {FL + A_2 E_2 \delta}{2A_1 E_1 + A_2 E_2}$

$$ \ $$ $L = 180×10^{-3} m$ 、 $\delta = 0.04 ×10^{-3} m$ 、 $F = 2000×9.81N$ 、

$A_1 = \displaystyle \frac {\pi}{4}×(8×10^ {-3})^2$ $m^ 2$ 、 $A_2 = \displaystyle \frac {\pi}{4}×(24×10^ {-3})^2$ $m^ 2$

となることに気を付けてください。

実際に代入すると、、、

$\lambda = 7.112947×10^{-5} m$

$\lambda = 0.0711 mm$

答えは $\lambda =0.0711 mm$ になります。(有効数字3桁です。)

できたでしょうか？代入の部分は自分で一度計算してみてください。

材料力学の不静定問題まとめ

材料力学不静定問題

今回は、材料力学でよく出てくる不静定問題中の内部応力について解説しました。

縮んだ量について等式を立てれたら後は簡単ですね。

長さを近似していい理由もしっかりと理解しましょう。

不静定問題以外にもはり、ねじりの問題も解説していますのでよかったらどうぞ！

合わせて読みたい！

また、解説してほしい材料力学の問題がありましたらFollow @OribiStudyのDMでご連絡ください。ありがとうございました。

おりびのブログ

「機械工or院卒→開発部」を目指す理系のためのブログ。

材料力学の不静定問題！よく出る不静定問題を４つのステップ毎に解説

材料力学の不静定問題

材料力学の不静定問題を解く４つの重要ステップ

材料力学の内部応力の解き方①：反力を仮定し力のつり合い式を立てる

材料力学の内部応力の解き方②：それぞれの丸棒の縮んだ量を考える

材料力学の内部応力の解き方③：縮んだ量について等式を立てる

材料力学の内部応力の解き方④：値を代入して計算する

材料力学の不静定問題まとめ

機械工のあなたにおすすめの記事

おりびのブログはリンクフリーです